电路笔记(一)
第一章 电路模型与电路定律
电路模型
理想电路元件是由实际电路元件建模抽象而成。
一般意义上的电路可以由三部分构成:激励、负载、线路。
两类电路:集总参数电路和分布参数电路
集总参数电路:实际电路尺寸远小于工作频率对应的信号波长,换句话说就是波长大得夸张,相比之下实际电路很小,这是实验室电路的场景。
分布参数电路:波长短至可以与电路元件尺寸相比拟,这就是集成电路/电力传输线的场景了。
现在学的电路这门课只是研究集总电路。
电流、电压和它们的参考方向
电流和电压
单位时间内通过导体横截面的电荷定义为电流。
-
单位正电荷在电场中在两点之间移动时的电场里做功叫电压/电位差。 -
电位:从某点到参考点的电压。(参考点的电位是0,有时候需要自己假设参考点)电位这个概念好像在以后的单片机编程里很重要。电位的高低是相对的,一万伏相对于9995伏也是高电位。
-
电动势:非电场力将单位正电荷从B移动到A所做的功(假如A是正极,B是负极的话),电动势只能是电源的自身性质。 是电位的升高,,而 。
为什么要有参考方向?
因为在复杂的电路中,电压或者电流的方向往往不确定,或者随时间变化。
可选择任意方向为参考方向,不一定与实际方向相同。因为在指定参考方向之后,实际方向就可以用正值和负值表示了。所以,和的正负只在指定的参考方向之下才有意义。
实线表示参考方向,虚线是实际方向。
关联与非关联
对某一段电路来说,电流参考方向与电压参考方向一致时,是关联参考方向。反之为非关联。
注意参考方向的关联与非关联只是针对某一二端元件或者某一段电路而言的,不可推广到整个回路。
从此刻开始,几乎所有电路参数都变成了变量,列式子时不必关心它们真正的正负,只需要关心它们参考方向的关联情况。
功率和能量
功率和功率的计算
关联参考方向时,;非关联时,。
说明该时刻元件吸收功率;说明放出功率。
功是功率对单位时间的积分。
关联参考方向时:
非关联参考方向时:
该公式中物理量的单位分别是、、和。
无源元件
如果对任意时刻 ,二端元件恒有 ,这个元件就叫无源元件。
啥意思呢,就是说这个元件吸收的功恒大于0,只能吸收能量,一点都不会放出能量,不算个电源。
电阻
阻值与材料电阻率、长度成正比,与横截面积成反比,还与温度系数有关。
分为线性和非线性两类。
线性电阻
在关联参考方向下, 成立(线性电阻的伏安关系),非关联时,。
电路元件两端之间电路物理量的代数函数关系叫端子特性(又叫元件特性)
线性电阻的伏安特性
通常特性曲线都是在关联参考方向下画的。
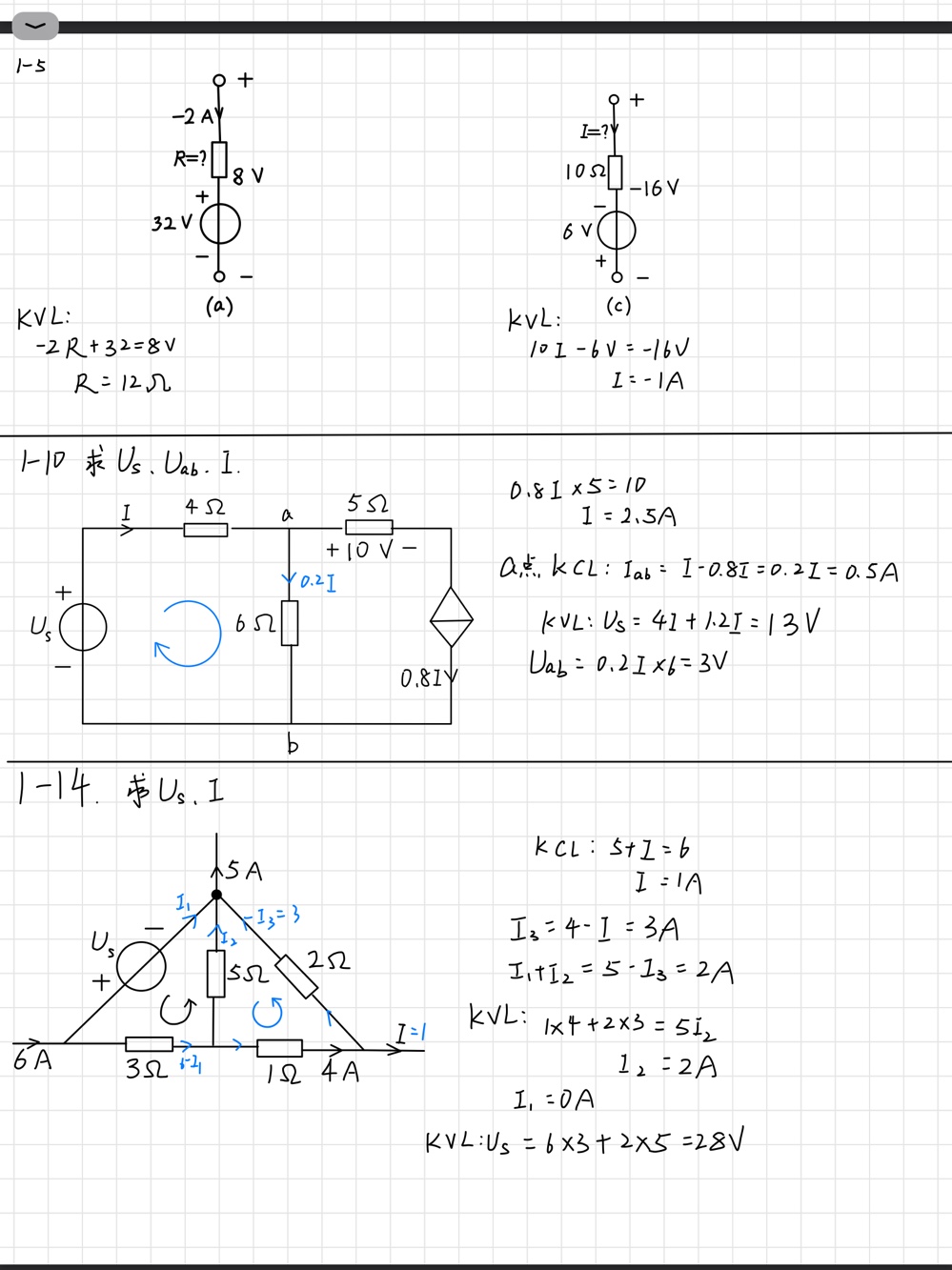
负电阻元件:会发出电能,电阻为负值,,伏安特性曲线位于二、四象限。
电导
单位是西门子(S)
电阻开路与短路下的伏安特性曲线
开路:,,此时图像表示为与u轴重合
短路:,,此时图像表示为与i轴重合
这里定义一下短路与开路:开路就是指,相应地,短路就是指。
电阻的功率
在关联参考方向下,线性电阻吸收的功率为
可以看出负电阻的功率是负值,说明它放出能量。
额定值
使电阻器正常运行的物理量的限额(上限)。
在额定电压下,若电气设备通过的电流高于额定值,则称为过载(过流),过载(过流)时间过长会使设备很快损坏;若电流低于额定值,则称为轻载,不能充分利用设备的能力,经济效益差。若电压低于额定电压,称为欠压运行,一般设备不能合理运行。如果电压超过额定电压,称为过压,会损坏设备。
电压源和电流源
理想电压源和电流源
-
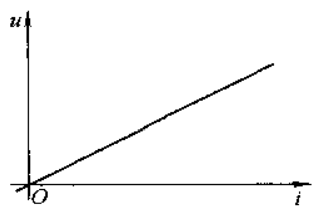
理想电压源的特点:
- 电压;
- 电流的大小和方向会随外电路的不同而改变;
- 内阻为0。
在非关联参考方向下画理想直流电压源的图时,值不会随值的变化而变化,是一条与轴平行的直线。
-
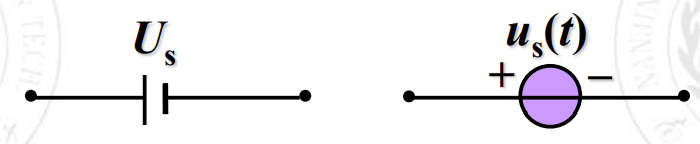
理想电流源的特点:
- 电流 ;
- 电压的大小和方向会随外电路的不同而改变;
- 内阻为。
(想一想是为什么)
在非关联参考方向下画理想直流电流源的图时,值不会随值的变化而变化,是一条与轴平行的直线。
实际电压源和电流源
-
实际电压源的电路模型
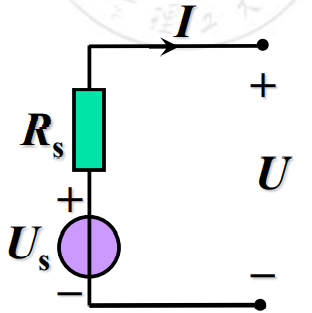
实际直流电压源输出电压都会随其电流的增大而降低。
即 。
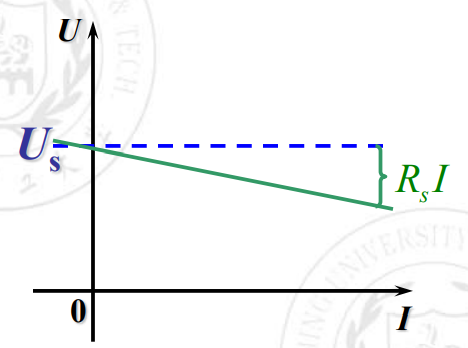
开路:,其中 是开路电压。
短路: 。其中是短路电流(就是图像上很远很远的那个点)
🔋短路时短路电流非常大!所以实际电压源不允许短路。
-
实际电流源的电路模型
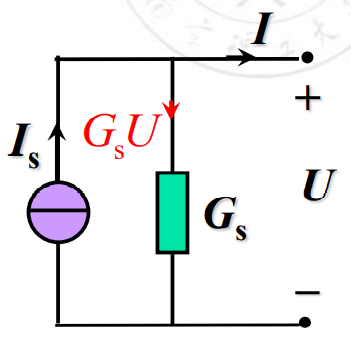
实际电流源输出电流会随电压的升高而减少
即 。
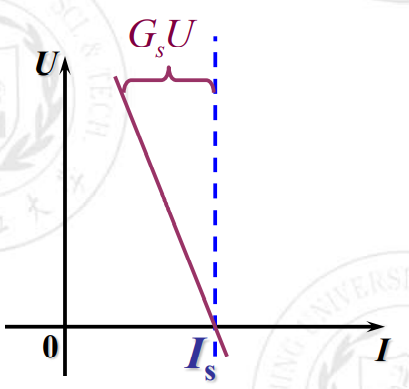
短路:
开路: 。(就是图像上很高很高的那个点)
开路时开路电压非常大,所以实际电流源不允许开路。
需要指出的是,我们一般很难去直接“造”一个电流源,因为**“电压是形成电流的原因”,**想要获得一个电流源到头来还是来调节这个电源的输出电压,开关电源的恒流模式,其实是通过对输出电压的精准控制来实现的。
独立源
电压/电流不受外电路的控制而独立存在的电源。只有这种电源可以在电路中起“激励”作用。
实际电路中,电压源不允许短路,电流源不允许开路。
理解和反思
MOOC上的问题:实际电流源的内阻Rs越小越好吗?
这里所说的“好”,是指电源在外电路不变时,自身消耗功率越小越好。所以,我们给电流源并联的电导两端的电压是不会变的,利用可以知道G越小,消耗功率越小。或者说恒流源可以理解成内阻越大越好的实际电源。
我们再来看理想电流源为什么内阻无穷大的问题。
电流源的内阻是并联的,内阻无穷大,就是电流源的电流全部供给外电路,没有内阻分流。
电压源的内阻是串联的,内阻无穷小,就是电压源的电压全部供给外电路,没有内阻分压。
受控源
上一节的独立源是电路中的“灵魂”,即电路中有了独立源,才能产生响应。
区别于独立源,受控源的电压(或者电流)值不是一个确定的量,其值是由控制源(电压或电流)的大小来决定的。所以,受控源又叫非独立源。它本身不能在电路中起到“激励”的作用,不能产生响应,但由于其可以向外输出电流电压的特性,被划分为“源”。
我理解的受控源,是从电压控制电压源VCVS开始的。不觉得很像一个变压器吗?它也是输入电压,吐出一个不同的电压。
进一步地,我们把四种受控源画成一个表格:
| 输出源类型\输入源类型 | 电压 | 电流 |
|---|---|---|
| 电压 | 电压控制电压源VCVS | 电流控制电压源CCVS |
| 电流 | 电压控制电流源VCCS | 电流控制电流源CCCS |
倒像一个电路中的物理量变换函数机器。
介于受控源需要获得电压/电流,我们的控制端需要设置成能够提供电压/电流的结构,这就能解释为什么控制端的旋钮对会是开路/短路的样子了。(建议对照下图理解)
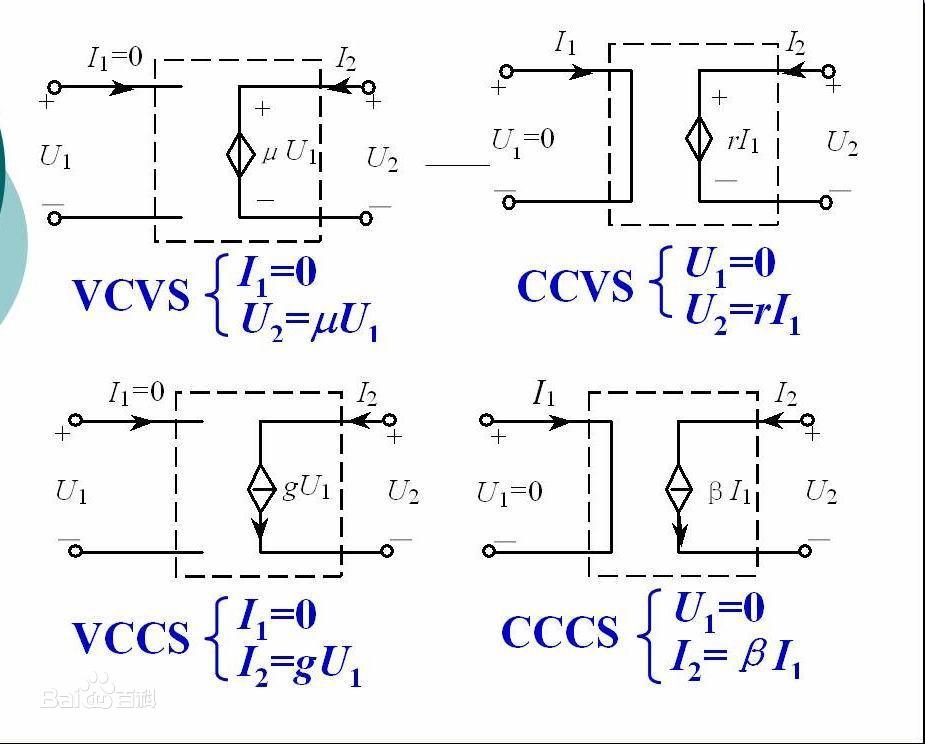
值得注意的是,实质上受控源的能量并不是来自控制信号回路,而是来自另外的电源供电。如上述的电流控制电流源,集电极的能量就来自外部的电源供电。当然,一般的三极管放大电路采用发射极和集电极共用电源的方式,这是一个特例。
思考与练习:
受控电流源的电流确定为不等于零时,其功率也一定不等于零。(错)
我的理解:我们只能知道这个电流源的电流不是0,并不知道它背后的供电系统发生了什么,以及这个电流源两端到底有没有电压。所以,我们也不知道它的功率到底是多少。
了解受控源“黑盒中的秘密”可以戳:https://www.zhihu.com/question/24303185/answer/1297340239
基尔霍夫定律(Kirchhoff’s laws)
支路和节点
关于节点的定义:
一本教材是:两个或者两个以上的元件具有的公共连接点,另一本教材上的定义是:三条或三条以上支路的连接点。
还有关于支路的定义:
一本书上说:每一个二端元件都叫支路,另一本书上说是:一个或多个二端元件串联组成的分支(即电流相同的一条支路)。
当然我们的教材用的都是第一种说法,即更小一点的节点和支路定义。
这是咋回事儿?
原来在尼尔森所著的《电路》里,是这样定义的:

🧭至此,疑问基本解决,我们只需要记忆我们书上所给的定义就好,不会再混淆了。
回路和网孔
由一条或几条支路组成的闭合路径称为回路。
平面电路图中,在回路内部不另含有支路的回路称为网孔。
为了用图论的办法去分析复杂电路,我们往往把有多个网孔的电路称作网络,有时网络和电路两个概念混用。
支路物理量的约束关系(受啥影响)
1.元件性质,比如电阻的阻值。
2.拓扑结构,就是元件之间相互连接的关系。基尔霍夫定律只表示这种关系。
上述两种约束是电路分析的基本依据。
基尔霍夫电流定律(KCL)
-
节点表述:在集总参数电路中,任何时刻流入或流出任一节点的所有支路电流的代数和等于零。即所有进入某节点的电流的总和,等于所有离开这节点的电流的总和。
流入的电流规定为负,流出的的电流为正。
我们都知道在电学里,大家喜欢拿
水和水管来比喻。🌊
那么基尔霍夫水管定律🌊:无论三通、四通的水管,流进去的水等于流出来水。(节点就是接头)
-
闭合面表述:任何时刻,对于一个封闭面流入或流出的电流代数和等于零。
引申的广义节点:在电路中随便画一个圈,这个圈可以认为是一个大的节点,那么流进圈内的电流也等于流出圈外的电流。
基尔霍夫电压定律(KVL)
-
真回路表述:沿着闭合回路所有元件两端的电势差(电压)的代数和
等于0。即任何时刻沿任一回路所有支路电压升等于所有支路电压降。注意:
① 列方程前标注回路绕行方向;
②如果规定电位降取正号,则电位升就取负号。
再拿水管比喻,电荷就像水,在电线中流动,会由电压高的地方向电压低的地方流动,产生电流,即为电势差。
基尔霍夫水管定律🌊又加一条,围成一圈并接在一起的水管内部水压和等于0。
-
假想回路表述:开口电压可按闭合回路来处理。
其实就是虚拟出一条在所求路径两端的一个支路,将该支路两端的电压“串接”到环路中即可。
如下图:
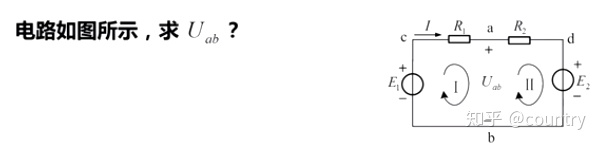
可将acba假想为一个闭合电路:

计算
值得注意的是,在列写方程式时,会出现两类正负号,一类是方程中物理量前面的正负号,另一类则是物理量本身数值的正负号。我们不用去关心物理量本身的正负,只需要基于基尔霍夫定律正确写出前面的正负号即可。
关于受控源:可以先将受控源看作是独立源,再代入控制量(就是之类的)求解。
作业