电阻电路的一般分析

第二章的等效变换法好用是好用，但毕竟会改变电路的结构，分析时还得看饭下菜，不够通用。这里会出现一些一般方法，也是KCL、KVL的延伸。

先导知识：电路的图结构

电路的图结构反映了电路的拓扑性质。
在图结构里，没有任何电路元件，只有抽象的线段，支路依赖于节点而存在。支路的形状不影响拓扑结构。
还记得在《电路笔记（一）》里面拿出来说的节点和支路吗？请注意，这里还是沿用着之前的概念，即元件两端为节点，节点交汇为支路，由此延伸出基本节点和基本支路的概念。

当图的任意两个节点之间至少存在一条路径时，这个图就是连通图。
一个连通图的树是指图的一个包含全部节点而不包含任一回路的连通子图。

确定一个树后，属于这个树的支路叫树支；
不属于这个树，但包含在图范围内的支路叫连支，所有连支叫补树。

一个连通图的树支数、连支数与它的节点数、支路数之间存在确定的关系。
如果这个树的节点数为 $n$ ，支路数为 $b$ ，则它的树支数为 $n-1$ ，连支数为 $b-n+1$ 。

我们想象一条不闭合路上的路灯，把节点比作路灯，把树支比作路灯间的空隙，那么每增加一个节点，就会多一条树支。所以树支数就是 $n-1$ 。所以树应是连接所有节点的最少支路的集合。
树支数和连支数的总和就是这个图所拥有的支路数，为 $b$ ，所以连支数为 $b-n+1$ 。回顾树的定义，树并不包含任何回路，所以每往树上加一条连支就会构成一条回路，这种回路叫单连支回路/基本回路。所以基本回路数等于连支数，为 $b-n+1$ 。

平面图里没有任何导线的跨越交叉。
内网孔内部区域内不再含有支路，这和我们的独立回路概念很像。
平面图的全部内网孔也是一组独立回路，其数目恰好是该图的独立回路数。

支路电流法

在这里，我们可能需要更换一下定义啦。
这里所谓的节点，是三条及三条以上支路的连接点，严谨点该叫它基本节点；
这里所谓的支路，是指流过相同电流的一条路，严谨点该叫它基本支路。
还没整明白的兄弟可以去看我的《电路笔记（一）》。

看了上边的先导知识，你觉得一个电路能列多少个KCL方程呢？哦，当然是n个，毕竟有n个节点嘛。
但是你列出来会傻眼——这些方程加起来，不还是0嘛！有啥用！
负责地说，这个方程组的秩（就是有效方程数）其实是 $n-1$ 。
所以只列 $n-1$ 个KCL方程就好啦。
剩的那个节点就叫参考节点，其他的叫独立节点。也就是说你要是指出哪个是参考节点，就要惨兮兮地把剩下 $n-1$ 个KCL方程列出来…
还记得我们在学等效电路之前，是怎么解决问题的吗？就是列一堆KCL和KVL方程，试图寻找答案。
你肯定会说，有几个回路列几个KVL方程嘛，这谁不会。
那白费功夫的就是你了。其实把独立回路的KVL列出来，其它的回路也不用列了，于是我们顺理成章地知道要列的KVL总数一定是 $b-n+1$ 。
记它干嘛？你只需要在电路图里数独立回路就完了，不用记的啊。

说了这么多，我们最终要列的方程数就是—— $n-1$ 个KCL方程加 $b-n+1$ 个KVL方程加 $b$ 个支路伏安关系方程。所以叫2b法。
别担心，列出这些个方程的你不是2b。我们可以把伏安方程和KVL方程合并嘛，这样就只剩b个方程啦！

所以2b法是咋列方程呢？

选出支路电流参考方向。
选一个参考节点，对剩下的列KCL方程。
选独立回路，指定绕行方向，开始列KVL方程。
解这 $b$ 个方程就完事啦。

要是电路里有电流源咋办呢？
给它安排一个电压呗，虚设电压，按电压源算。再不济，选独立回路的时候不带它玩不就行了嘛。这就是两招儿了。

网孔电流法和回路电流法

其实支路电流法的方程也还挺多的，想简化一下。
不知道你们在看电路图的时候，会不会有一种把回路里不同支路上的电流全部同化的冲动。那就跟着这个想法，搭建出来我们的理想电路分析方法吧。
网孔是啥希望你还记得。
假设网孔边界的电流就是网孔电流，那么网孔交汇处的支路电流就是几个网孔电流相互影响下的结果，简单来说就是代数和。所以电路中所有的支路电流都能用网孔电流来表示。只需要求解网孔电流就可以把电路里所有的电流信息掌握在手里。呵，鸭头，你跑不掉的。
综上所述，网孔电流是一组完备的独立电路变量。
根据之前的思路，网孔电流和支路电流之间的关系就体现了KCL，所以只需要拿网孔电流当变量，列出来KVL方程就好啦。这叫网孔电流方程。
网孔电流法的本质就是KVL方程。
回到正题，俺们懒人是要减少工作量的，这个方法要列几个方程啊？
网孔数有 $b-n+1$ 个，只要列这么多就好啦，工作量瞬间减去了 $n-1$ 个方程，有被爽到。
所以咋列啊？
先写写KVL方程呗。
写出来长这样：

整理之后的网孔电阻矩阵是个对称矩阵诶。
咱来找一下电阻出现的规律。

缩写	数学含义	正负判断
$R_{kk}$	网孔电阻之和	恒为正
$R_{kj}$	两网孔间的互电阻	相邻网孔电流在公共支路上流向一致时为正
$u_{skk}$	电压源电压的代数和	与网孔电流关联方向时为负

看出来规律之后列方程，懂的都懂。
步骤大概是：

选网孔电流和参考方向。
按规律写网孔电流方程。
解就完了。

还是同一个问题，电流源来了咋办？
看情况啊。

要是电流源跟电阻并联，想想实际电流源的等效变换。
要是电流源孤零零的没有并联伙伴，给它设个电压，当电压源呗，算的时候归到等式右边不就完了。
要是电流源自己在电路边缘待着，一个人撑起一整个网孔电流，已知网孔电流，你不就能少列一个方程了嘛。

电路里有受控源时，先把受控源看成独立源，列完方程再把控制量用未知量表示，代回去算就完了。
wkdlsky
注意：含受控源时，两网孔之间的互电阻不相等，即 $R_{12}\neq R_{21}$ 。

还记得独立回路是啥不？
在电路里选一系列回路，每一次选择的回路中都有一条原先选择的回路所没有的新支路，那么这一系列回路叫独立回路。
每定义一个独立回路，之中必须、至少有一条未被使用过的支路，直到所有的支路都被用过为止，这样列写出的方程才能保证都是独立方程且联立求解时可求出未知量。
例如一个“日”字形结构的电路，它有三个回路，但独立回路只有两个。这两个独立回路可以是两个小“口”字形的回路，也可以是一个小“口”字形加最外围的闭合回路。

回到刚才给网孔电流法补bug的思路——如果电流源在电路中间，还得给这位大爷虚设电压。
我一边痛骂自己可真够懒的，一边思考：啥法子能让它变成回路边缘呢？
那就不用网孔呗，反正网孔也是一组独立回路，我换一组别的独立回路不就完了。
于是，回路电流法诞生了。自由的我开心了。

回路电流是在一个回路中连续流动的假想电流，也就是在那个独属于它的新支路上流动的电流。
与网孔电流相似，它们也是一组独立、完备的电路变量。
回路的选取应本着“使每个电流源支路仅包含在一个回路中”的原则。

网孔一定是独立回路，独立回路不一定是网孔。所以回路电流法是网孔电流法在平面上的应用，网孔电流法是回路电流法的特例。
列写回路电流的步骤可以类比网孔电流，此处不再赘述。

节点电压法

不知道你们有没有遇到过电路中有一个节点接地的情况。反正用easyEDA仿真的时候，不接地就不给仿真，可给我无语坏了，只能乖乖听人家的。

那还有电流啥事儿啊？直接拿接地的一端当参考点，找其它节点的相对电压不就完了。这跟电位的概念倒是很接近。
这里的节点指三条及三条以上支路的连接点，再强调一遍。
说干就干。
咱把参考节点当负极性端，其它节点当正极性端，看看能不能拿这些个电位差当变量列方程。
节点的英文是node，咱就把其他节点电压设成 $u_{n1}$ 、 $u_{n2}$ 、 $u_{n3}$ 好了。

回忆一下网孔电流法，用网孔电流当变量来表示支路电流。
通过类比，我们试图从节点电压来扩大它们在电路图中的“人脉关系”，以求能普遍表示一些变量。
幸运的是，电路中每一条支路两端都有两个节点，支路电压就是节点电位差。
这样，我们就可以拿节点电压当变量，把所有的支路电压表示出来。

等一下，这个拿节点电压当变量的思路不就是KVL吗？
那再列个KCL方程组不就可以完美求解电路了吗？
所以说节点电压法的本质就是KCL方程。

现在场外求助一下支路电流法，它说，学它列 $n-1$ 个KCL方程呗。
从第一步开始copy，把参考节点也选了。
既然参考节点要跟尽量多的节点联系上，那最好还是选连结支路数最多的节点嘛。
拿电导开始列方程，化简：
111

震惊地发现是跟网孔电流法基本一样的对称矩阵。啥都挺像，你俩组个cp得了。
咱来找一下电导出现的规律。

缩写	数学含义	正负判断
$G_{kk}$	节点周围的电导之和	恒为正
$G_{kj}$	两节点公共支路上的互电阻	一律为负
$I_{skk}$	流入该节点的所有电流源电流的代数和	流入取正

下面开始找bug时间。

Q1：一条支路上有俩电导咋办？
A1：用 $G=\frac{G_1G_2}{G_{1}+G_{2}}$ 代替呗。

Q2：有电压源咋办？
A2：类比网孔电流法含电流源，可以找到解决方案如下。

要是电压源跟电阻串联，想想等效变换。
要是电压源都跟参考节点挨着，一个人撑起一整个节点电压，已知节点电压，你不就能少列一个方程了嘛。
要是有好几个电压源，实在没办法全安排到参考节点身边，给它设个电流，当电流源呗，算的时候归到等式右边不就完了。

Q3：有控制源咋办？
A3：这位同学，一看你上边网孔电流法的受控源处理就没咋看。步骤一模一样的诶。

Q4：电流源串联电阻咋办？
A4：请问你还记得等效法吗。电流源跟电阻串联，直接就可以忽略这个电阻的…把它当小透明就好，结论就是与电流源串联的电阻不出现在自导或互导中。

补充一个弥尔曼定理（就是电路里只有俩节点的情况）：
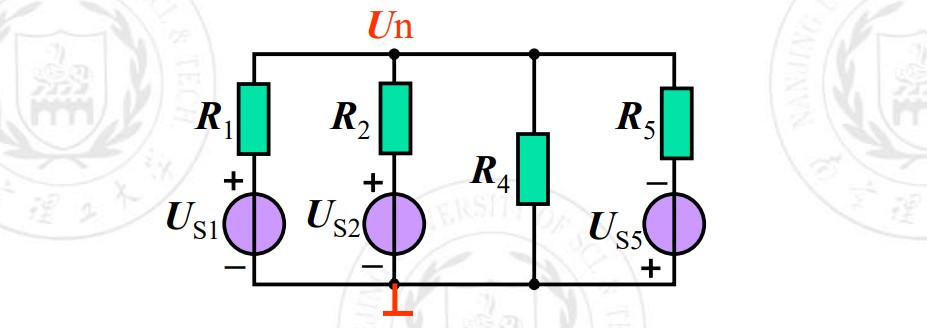
memdl

列完节点电压法方程再化简长这样

$U_{\mathrm{n}}=\frac{\frac{U_{\mathrm{Sl}}}{R_{1}}+\frac{U_{\mathrm{S} 2}}{R_{2}}-\frac{U_{\mathrm{S} 5}}{R_{5}}}{\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{4}}+\frac{1}{R_{5}}\right)}$

简单写就是

$U_{n}=\frac{\sum I_{S}}{\sum G}$

其实也没啥了解必要，挺简单，就顺便提一嘴。俺自己本来就不太喜欢公式化的东西，但毕竟人家简洁…多一个公式少十个读者嘛。

好啦第三章就写到这里，码字不易，欢迎多评论挑错哦。