基本概念

  • 完整性是指信息未经授权不能进行改变的特性，即信息在存储或传输过程中保持不被偶然或蓄意地删除、修改、伪造、乱序、重放、插入等破坏和丢失的特性。
  • 影响信息完整性的主要因素有：设备故障、误码（传输、处理和存储过程中产生的误码，定时的稳定度和精度降低造成的误码，各种干扰源造成的误码）、人为攻击、计算机病毒等。
  • 保证信息完整性的主要方法包括以下几种：
    协议：通过各种安全协议可以有效地检测出被复制的信息、被删除的字段、失效的字段和被修改的字段。
    纠错编码方法：由此完成检错和纠错功能。最简单和常用的纠错编码方法是奇偶校验法。
    密码校验和方法：抗篡改和传输失败的重要手段。
    数字签名：保障信息的真实性。
    公证：请求网络管理或中介机构证明信息的真实性。

RFID系统的数据传输出错

干扰原因：系统内部的热噪声和系统和外部的各种电磁干扰等

读写器->电子标签传输错误：

  1. 电子标签错误的响应读写器的命令；
  2. 电子标签的工作状态发生混乱；
  3. 电子标签错误的进入休眠状态。

电子标签->读写器传输错误：

  1. 不能识别正常工作的电子标签，误判电子标签的工作状态；
  2. 将一个电子标签判别为另一个电子标签，造成识别错误。

解决方法：

  1. 加大读写器的输出功率，提高信噪比，但可能会造成电磁污染。
  2. 在原始数据后加上一些校验位，接收端根据判断收到的数据位和校验位之间是否满足这种关联关系来判断有没有发生畸变，这就是差错控制编码。

差错控制方式

  • 差错分为随机错误和突发错误。随机错误由热噪声引起，突发错误由冲击噪声引起。

  • 衡量指标有误码率（差错码元数与收到的总码元数之比）和误信率（差错比特数与总比特数之比）
    image.png

  • 差错控制方式：常用的差错控制方式主要有检错重发（简称ARQ），前向纠错（简称FEC），混合纠错（简称HEC）。
    重点看区别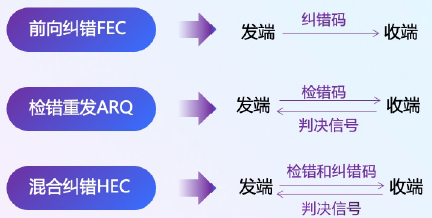：image.png

差错控制编码

  • 纠错编码分为检错码和纠错码。检错码以检错为目的，不一定能纠错；而纠错码以纠错为目的，一定能检错。
  • 监督码元：发送端在信息码元序列中增加的差错控制码元。
  • 多余度：用来衡量监督码元个数。例如，若平均每两个信息码元就添加一个监督码元，则这种编码的多余度为1/3。
  • 编码效率(简称码率) ：设编码序列中信息码元数量为k，总码元数量为n，则比值k/n 就是码率。
  • 冗余度：监督码元数(n-k) 和信息码元数 k 之比。
  • 禁用码组和许用码组
  • 在分组码中，非零码元的数目称为码字的汉明重量，简称码重。例如，码字 10110，码重w=3。
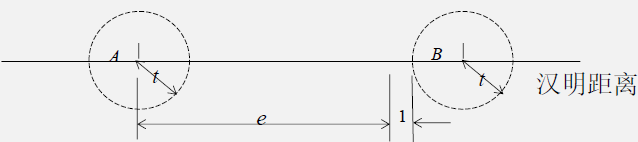
  • 码距：把两个码组中对应位上数字不同的位数称为码组的距离。码距又称汉明距离。例如000，011，101，110，4个码组间任意两个的距离均为2。
  • 最小码距：把某种编码中各个码组之间距离的最小值称为最小码距，用d0d_0表示。最小码距是码的一个重要参数， 它是衡量码检错、纠错能力的依据。

检纠错码的分类

  • 按误码原因：纠正随机错误码与纠正突发错误码。
  • 按约束方式：分组码和卷积码。卷积码的监督码元不仅与本组的信息码元有关，还与前面若干组的信息码元有关。
  • 按功能：检错码和纠错码
  • 按编码前后变化：系统码（编码后的信息码元不发生变化，且与监督位分开）和非系统码（信息码元发生变化）。
  • 按数学关系：线性码和非线性码。

汉明码

又叫线性分组码，它是一种能够自动检测并纠正单个错误的线性纠错码。
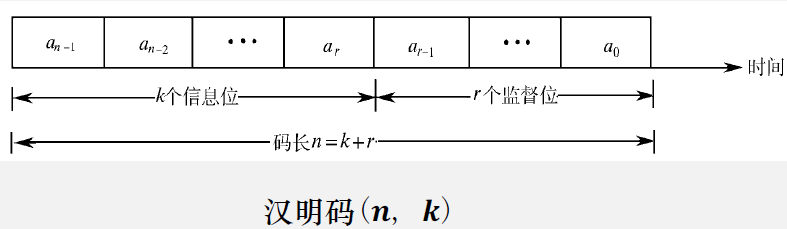
image.png

汉明不等式：设信息位个数k，监督位r，码长为n=k+r，
则汉明不等式为 2r−1≥n2^r-1\ge n 或 2r≥k+r+12^r\ge k+r+1 。

码距与编码纠错能力的关系（重要）

  • 为检测e个错码，要求最小码距d0≥e+1d_0\ge e+1
  • 为纠正t个错码，要求最小码距d0≥2t+1d_0 \ge 2t + 1。
  • 为纠正t个错码，同时检测e个错码，要求最小码距d0≥e+t+1(e>t)d_0\ge e+t+1(e>t)
    image.png

奇偶校验法

奇偶校验法是在原信息码后面附加一个监督元，使得码组中“1”的个数是奇数或偶数。分为奇校验法和偶校验法。
常用的奇偶检验法为垂直奇偶校验、水平奇偶校验和水平垂直奇偶校验。
例：若信息码元为100101，试求：
（1）奇监督码；0
（2）偶监督码；1
（3）编码的效率；n/(n+1)
（4）若有1位错码，能检测吗？能
（5）若有2位错码，能检测吗？不能

循环冗余校验（CRC）

  • 循环冗余校验码由信息位和校验位两部分组成。若信息位为k位, 校验位为r位, 则该校验码被称为(k＋r, k)码。
  • 假设待编码的有效信息以多项式M(X)表示，将它左移若干位后，用另一个约定的多项式G(X)去除，所产生的的余数R(X)就是校验位。有效信息和校验位相拼接就构成了CRC码。这里的G(X)称为生成多项式。
    编码步骤：
  1. 将待编码的k位有效信息位表示为一个k－1k－1阶的多项式M(X)。
  2. 将M(X)左移r位, 得到M(X)⋅XrM(X)·X^r（rr由预选的r+1r+1位的生成多项式G(X)决定）。
  3. 用一个预选好的r+1r+1位的G(X)对M(X).XrM(X).X^r作模2除法。
  4. 把左移r位后的的有效信息位与余数作模2加法, 形成长度为k+rk+r的CRC码。

M(X)⋅Xr＋R(X)＝Q(X).G(X)M(X)·X^r＋R(X)＝Q(X).G(X)

image.png
image.png

  • 选择生成多项式的要求
    任何一位出错都应使余数不为0。
    不同位出错应使余数不同。
    对余数继续作模2除法，应使余数循环。
  • 常用的生成多项式：
    CRC−12＝X12+X11+X3+X2+X+1CRC-12 ＝X^{12}+X^{11}+X^3+X^2+X+1
    CRC−16＝X16+X15+X2+1CRC-16 ＝X^{16}+X^{15}+X^2+1
    CRC−CCITT＝X16+X12+X5+1CRC-CCITT＝X^{16}+X^{12}+X^5+1
    image.png

习题

image.png