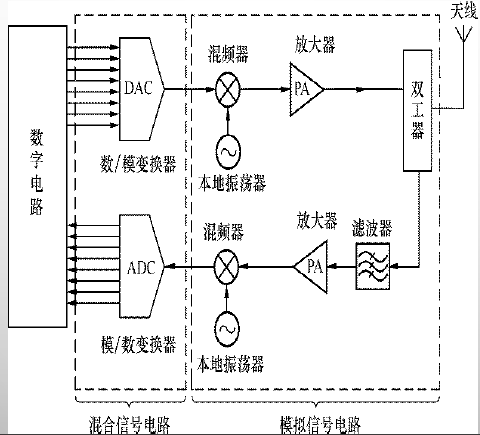
实现射频能量和信息传输的电路称为射频前端电路，简称为射频前端

读写器天线电路

串联谐振时，电路可获得最大的回路电流。

谐振条件

X=ωL−1ωC=0X=\omega L-\frac{1}{\omega C}=0

此时，角频率为ω0=1LC\omega_0=\frac{1}{\sqrt{LC}}，频率为f0=12πLCf_0=\frac{1}{2\pi\sqrt{LC}}
特性阻抗为ω0L=1ω0C=LC=ρ\omega_0L=\frac{1}{\omega_0C}=\sqrt{\frac{L}{C}}=\rho
品质因数Q为

Q=ω0LR=1ω0CR=1RLC=1RρQ=\frac{\omega_{0} L}{R}=\frac{1}{\omega_{0} C R}=\frac{1}{R} \sqrt{\frac{L}{C}}=\frac{1}{R} \rho

通频带BW为

BW=ω2−ω12π=ω02πQ=f0Q=2(ω2−ω0)2π=2Δω0.72π\begin{array}{l} \mathrm{BW}=\frac{\omega_{2}-\omega_{1}}{2 \pi}=\frac{\omega_{0}}{2 \pi Q}=\frac{f_{0}}{Q} \\ =\frac{2\left(\omega_{2}-\omega_{0}\right)}{2 \pi}=\frac{2 \Delta \omega_{0.7}}{2 \pi} \end{array}

例4.1 某高频RFID工作频率为13.56MHZ，采用串联谐振的射频前端电路：
（1）若线圈天线的电感为1.0 H，求串联电容C。
（2）若串联谐振电路的品质因数为20，求串联电阻R。
（3）计算串联谐振电路的频带宽度。

电感线圈的交变磁场

磁场强度H 、磁感应强度B

对于直线载流体，在半径为A的环行磁力线上，磁场强度H是恒定的，磁场强度H与磁感应强度B分别为

H=i2πaH=\frac {i}{2\pi a}

B=μ0μrHB=\mu_0\mu_rH

μ0μ_0为真空磁导率=4π×10−7H/m4π×10^{-7}H/m
μrμ_r为相对磁导率

环形短圆柱形线圈的磁感应强度

  1. B与R的关系
    离线圈中心距离为r处P点的磁感应强度的大小为

Bz=μ0i1N1a22(a2+r2)3/2=μ0HzB_z=\frac{\mu_0i_1N_1a^2}{2(a^2+r^2)^{3/2}}=\mu_0H_z

其中，N1为线圈匝数
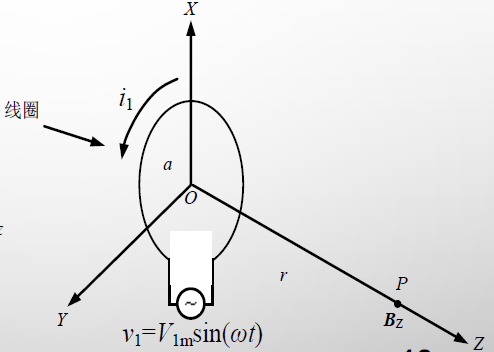
image.png
从线圈中心到一定距离磁场强度几乎是不变的，而后急剧下降
2. 最佳线圈半径A（重要）
设R为常数，并简单地假定线圈中电流不变，讨论A和BZ的关系。
结论：当r一定时，在a=2ra = \sqrt2r处可获得最大场强

电子标签天线电路

并联谐振时，回路两端可获得最大的电压。

谐振条件

条件跟并联一样，都是祖传公式。
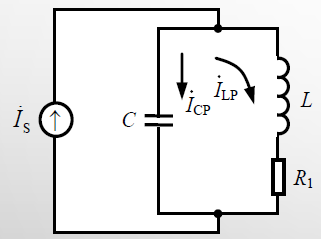
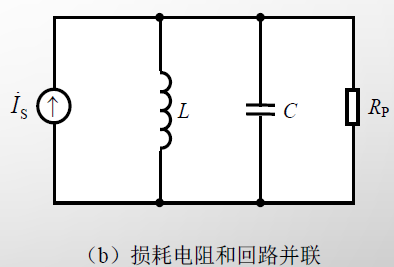
image.png

image.png

并联谐振回路谐振时的谐振电阻RPR_P为纯阻性。

RP=LCR1=ωP2L2R1R_P=\frac{L}{CR_1}=\frac{\omega_P^2L^2}{R_1}

品质因数

QP=ωPLR1=1ωPR1C=1R1LC=1R1ρQ_P=\frac{\omega_PL}{R_1}=\frac{1}{\omega_PR_1C}=\frac{1}{R_1}\sqrt{\frac{L}{C}}=\frac{1}{R_1}\rho

其中，ρ\rho为特性阻抗
通频带带宽为

BW=2Δω0.72π=2Δf0.7=fPQPBW=2\frac{\Delta\omega_{0.7}}{2\pi}=2\Delta f_{0.7}=\frac{f_P}{Q_P}

image.png

电感耦合

负载调制

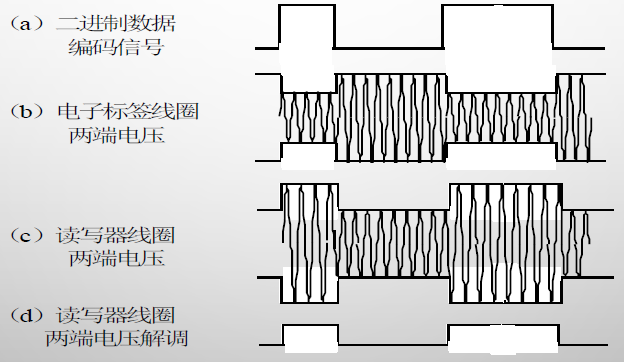
在RFID系统中，电子标签向读写器的信息传输采用负载调制技术。
负载调制通过对电子标签振荡回路的电参数按照数据流的节拍进行调节，使电子标签阻抗的大小和相位随之改变，从而完成调制的过程。
负载调制技术主要有电阻负载调制和电容负载调制两种方式。

  1. 电阻负载调制
    原理：开关S用于控制负载调制电阻RMOD的接入与否，开关S的通断由二进制数据编码信号控制。
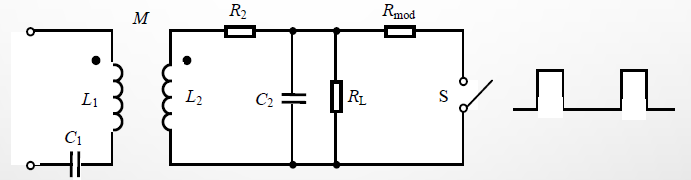
    image.png
    当电子标签谐振回路两端的电压发生变化时，由于线圈电感耦合，这种变化会传递给读写器，表现出读写器线圈两端电压的振幅发生变化。电阻负载调制过程是一个调幅过程。
    image.png

  2. 电容负载调制
    电容负载调制是用附加的电容器Cmod代替调制电阻Rmod。其中，R2是电感线圈L2的损耗电阻。
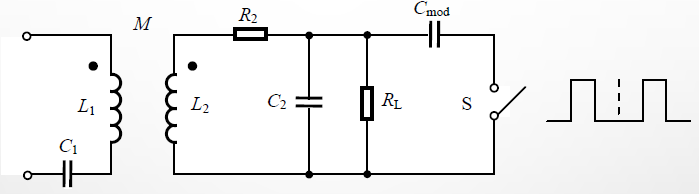
    image.png
    开关的通断控制电容按数据流的时钟接通和断开，使电子标签的谐振频率在两个频率直接转换。电容Cmod的接入使电子标签电感线圈上的电压下降。电容负载调制中，读写器电感线圈上电压不仅发生振幅的变化，也发生相位的变化。

习题

image.png
image.png

滤波器设计

RFID的射频前端

需要记有哪些模块
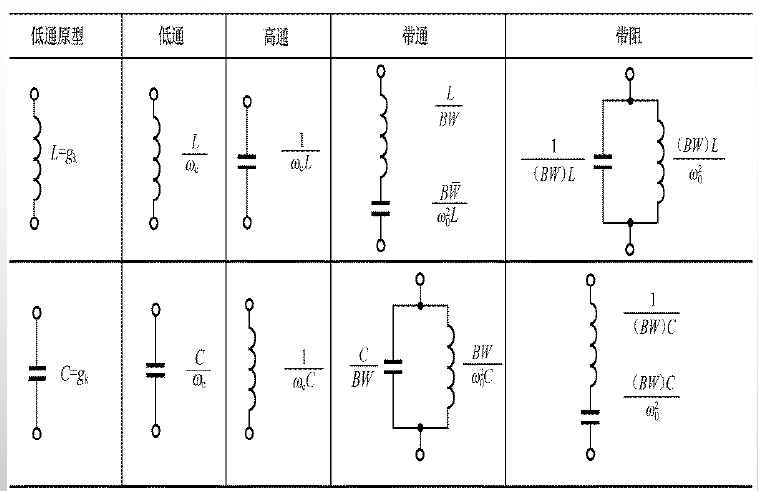
image.png

低通原型

插入损耗定义为来自源的可用功率与传送到负载功率的比值

IL=10lg11−∣Γin(ω)∣2IL=10lg\frac{1}{1-\left | {\Gamma_{in}{(\omega)}}\right | ^2}

巴特沃斯

如果滤波器在通带内的插入损耗随频率的变化是最平坦的，这种滤波器称为巴特沃斯滤波器。

IL=10lg[1+k2(ωωc)2N]IL=10lg[1+k^2(\frac{\omega}{\omega_c})^{2N}]

ωc\omega_c是截止角频率，N是滤波器阶数
N值越大，阻带内衰减随着频率增大得越快。设计低通滤波器时，对阻带内的衰减有数值上的要求，由此可以计算出N值。（有个图可以查）
元件取值也有表可以查。

切比雪夫

如果滤波器在通带内有等波纹的响应，这种滤波器称为切比雪夫滤波器。

IL=10lg[1+k2TN2(ωωc)]IL=10lg[1+k^2T_N^2(\frac{\omega}{\omega_c})]

阻带内衰减随着频率的升高单调上升

椭圆函数低通滤波器原型

线性相位低通滤波器原型

滤波器变换

对低通滤波器原型进行反归一化设计，可以变换到任意源阻抗和任意频率的低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
滤波器的变换包括阻抗变换和频率变换2个过程。
image.png

放大器设计

放大器稳定意味着反射系数的模小于1。
输入输出电压驻波比

VSWR=1+∣Γ∣1−∣Γ∣VSWR=\frac{1+\left|\Gamma\right|}{1-\left|\Gamma\right|}

噪声系数

输入信号的信噪比与输出信号的信噪比之比：

F=PSi/PNiPSo/PNoF=\frac{P_{Si}/P_{Ni}}{P_{So}/P_{No}}

F=F1+F2−1GA1+F3−1GA1GA2+⋯+Fn−1GA1GA2⋯GAn−1F=F_{1}+\frac{F_{2}-1}{G_{A 1}}+\frac{F_{3}-1}{G_{A 1} G_{A 2}}+\cdots+\frac{F_{n}-1}{G_{A 1} G_{A 2} \cdots G_{A n-1}}

多级的级连的高增益放大器，仅第一级对总噪声有较大影响。

射频功放设计

  1. 1dB增益压缩点
    当晶体管的功率增益从其小信号线性功率增益下降1dB时，对应的点称为1dB增益压缩点。
  2. 1dB增益压缩点定义的动态范围
    功率放大器的动态范围是指接收机能容忍的最大信号与最小信号功率之比。最小信号功率可以取噪声基底功率，最大信号功率可以取1dB增益压缩点。
  3. 交调失真
    在非线性放大器的输入端加两个或两个以上频率的正弦信号时，在输出端将产生附加的频率分量。这些新的频率分量称为谐波失真或交调失真。
  4. 3阶截点IP3
    多个正弦信号输入后，由于放大器的非线性作用，输出三阶交调分量的功率电平最大。三阶截取点(IP3)是表示线性度或失真性能的参数。