电路笔记（二）

第二章 简单电阻电路分析

等效变换和串并联

电路分析中有很多典型而简单的分析方法，比如混联电路的分析、平衡电桥。但同时我们发现很多问题是不能简单地进行求解的，所以我们还要讨论一些网络等效的方法，包括网络的等效、电源等效，etc。

线性元件$\rightarrow$​线性电路$\rightarrow$​线性电阻电路。

一端口电路（网络）= 二端电路（网络）= 具有一对端钮的电路

两个一端口网络等效：对外部而言在端口处的伏安关系完全相同；但对内部而言，结构是不同的。这种等效可以使两个一端口网络对于外电路来说互相替代，所以又叫等效变换，缩写为$eq$​​。

$R_{eq}$是等效电阻的意思。

那三端和很多端的电路咋用等效化简呢？

请注意，我们的等效概念可以推广到它们，即等效是指两个多端电路对应端钮处的$U-I$​关系式完全相同。

在这里，所有的等效和变换都是为了电路分析和计算的方便，这就是它们的用处。当然，到后面会有更加好用的工具，俺们懒人不妨期待一下。

串并联

1. 串联

对串联回路使用KVL，得到串联电阻的阻值：

$$R_{eq}=\sum^n_{k=1}R_k$$

即串联电路的总电阻等于各分电阻之和

由Ohm定律，串联分压规律：

$$u_k=R_ki=\frac{R_k}{R_{eq}}u$$

电压与电阻成正比，因此串联电阻电路可作分压电路。

2. 并联

对并联节点使用KCL，可得并联的电导：

$$G_{p}=\sum G_{k}$$

即等效电导等于并联的各电导之和。

由电导的Ohm定律，并联分流规律：

$$\frac{i_{k}}{i}=\frac{G_{k}}{G_{p}}$$

电流分配与电导成正比。

三个电阻并联：$R_{eq}=\frac{R_1R_2R_3}{R_1R_2+R_2R_3+R_1R_3}$​​

3. 对偶性：

   电阻串联和电导并联都有对偶性。这些可以相互转换的元素叫对偶元素，这两个关系式叫对偶关系式。

串并联简化方法

如何判断串并联关系？

通过节点的移动和元件的拉伸。

• 字母标注法的使用

  

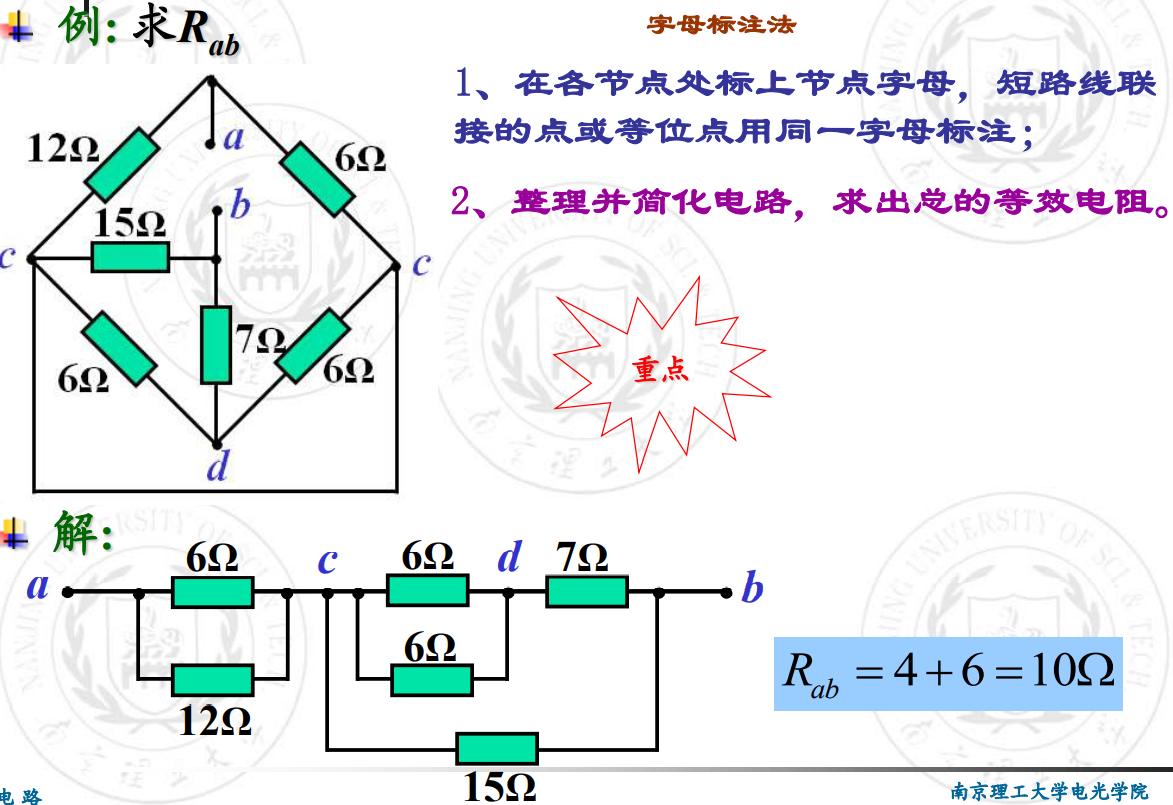
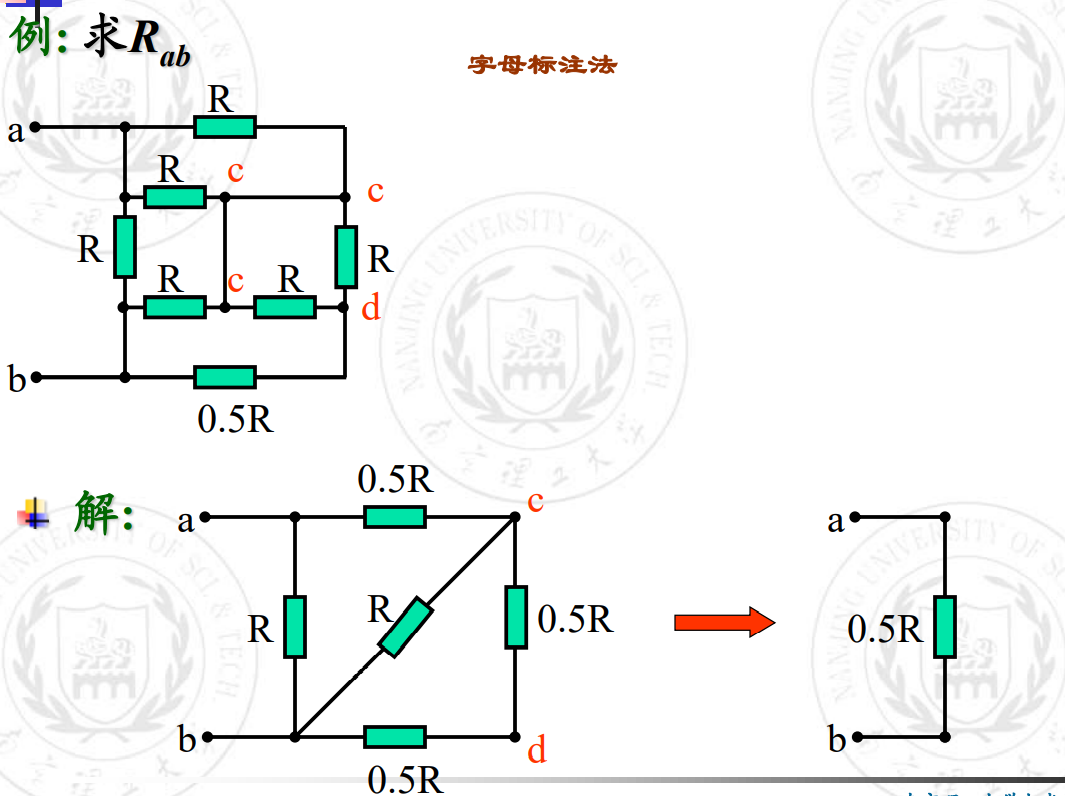
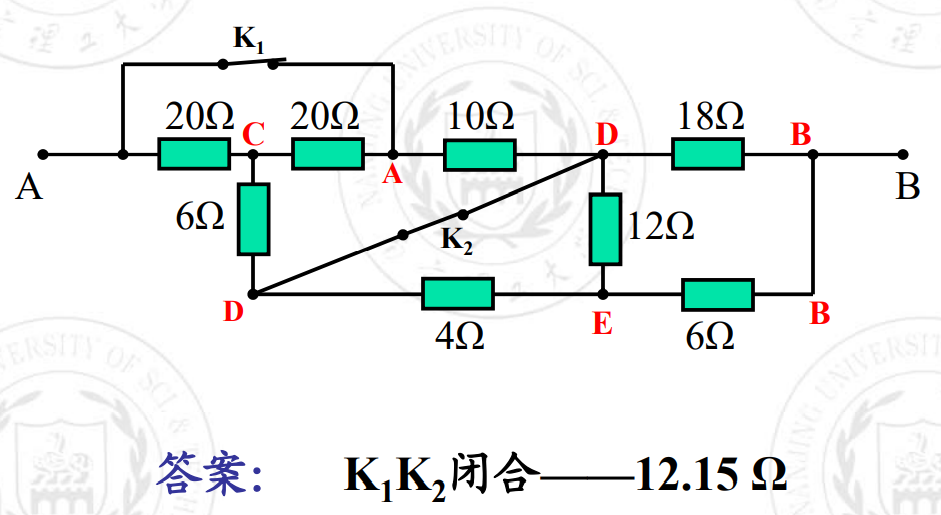
熟悉了吗？来算算这道：

电桥和平衡电桥

电桥的识别

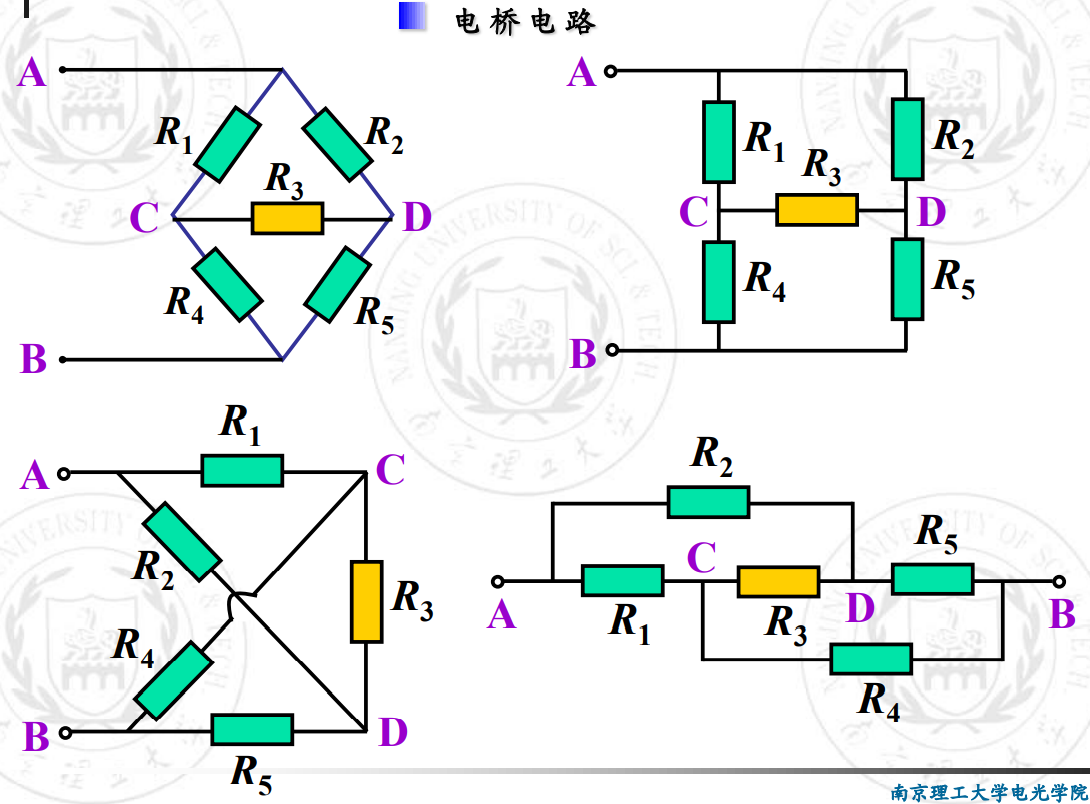
电桥判据12345
1套电桥
2条最短路径
每个节点3条连线
4个元件参与分压
电桥总共5个元件

又比如如下绿色区域，形状接近但并不是电桥：

因为如图的红点上链接了四条线。

电桥平衡（等电位）

由分压规律：

$$\begin{array}{c} U_{A}=\frac{R_{2}}{R_{1}+R_{2}} \\ U_{B}=\frac{R_{4}}{R_{3}+R_{4}} \end{array}$$

如果$R_{1} R_{4}=R_{2} R_{3}$​​，那么AB两点是等电位点。从而中间连入的电阻没有电流通过。因而这个平衡电桥简化为简单的串并联结构。

平衡电桥可以认为是并联的串联，也可以看成串联的并联。

根据我们的经验，当某条支路电流为零时，我们可以把它等效为断开；当某条支路电压为零时，我们可以把它等效为短路。

平衡电桥中间电阻两端电压为零，流过的电流也为零，所以遇到这种情况时我们有两种处理方式：

把中间支路短路或者断开，正经点儿就叫既可开路又可短路。

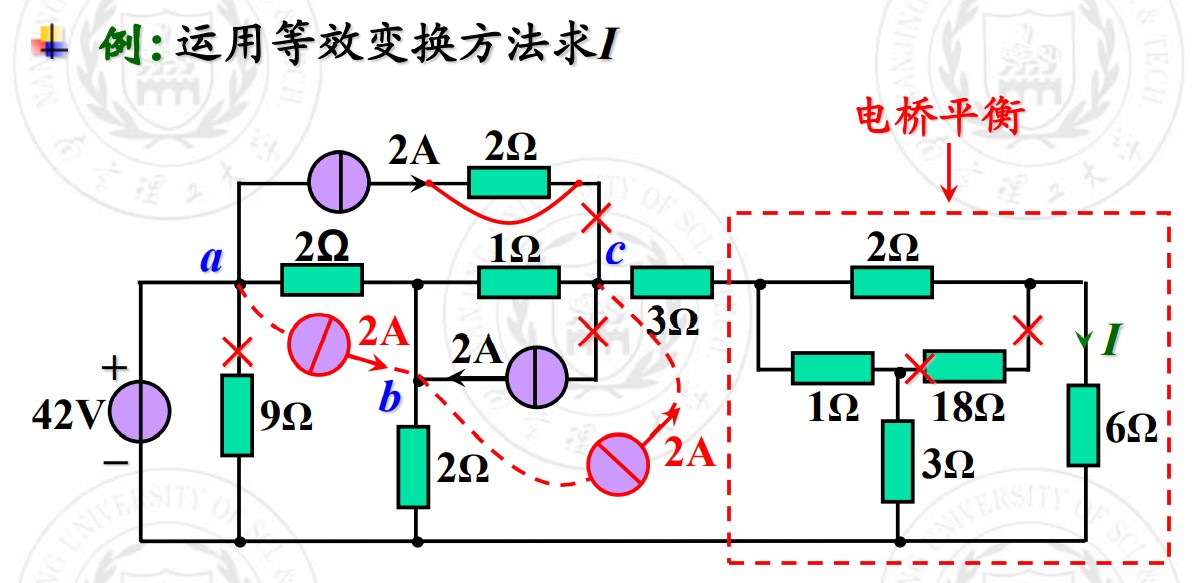
来看例题：

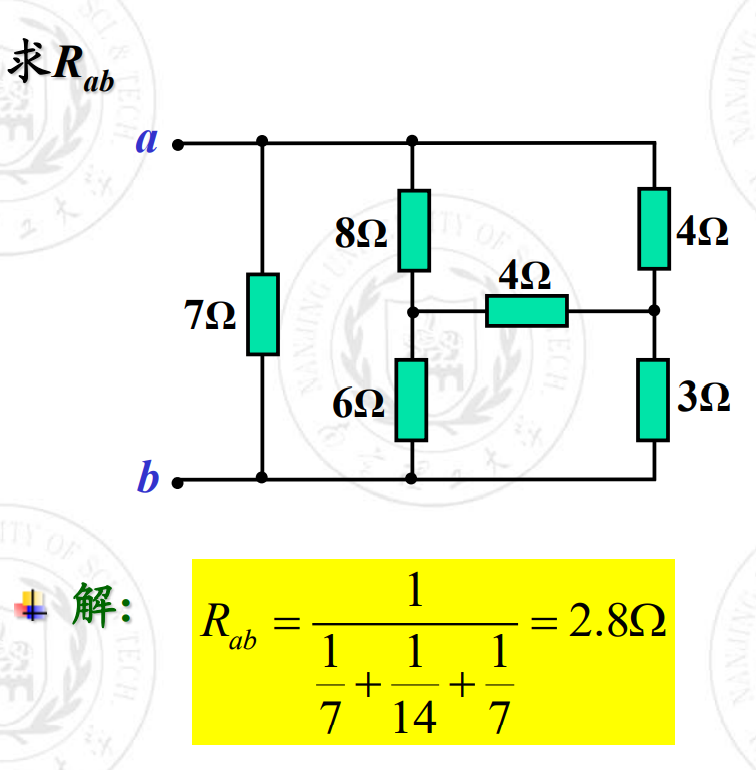
再看一道加深对等电位的理解：

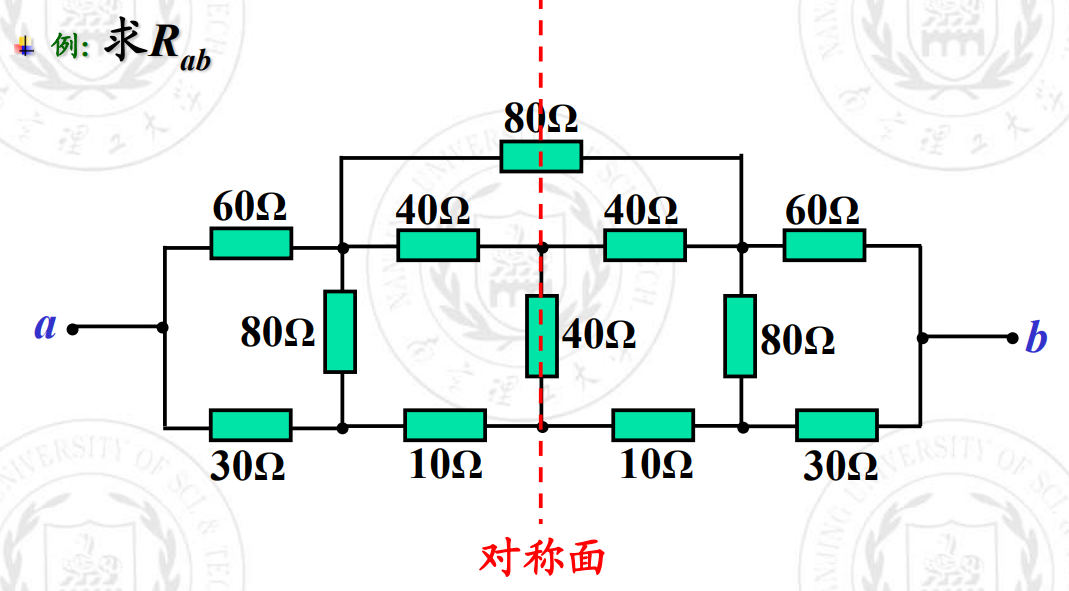
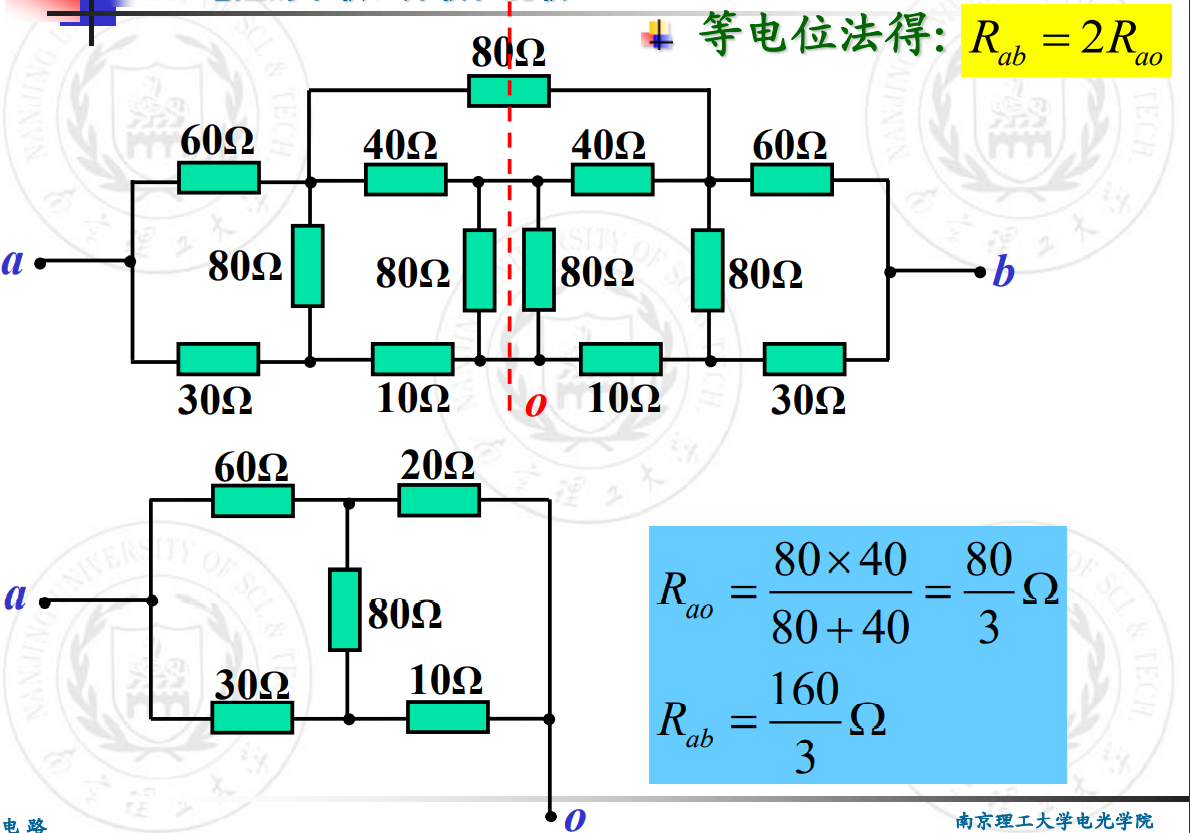
无限长梯形电阻网络的计算

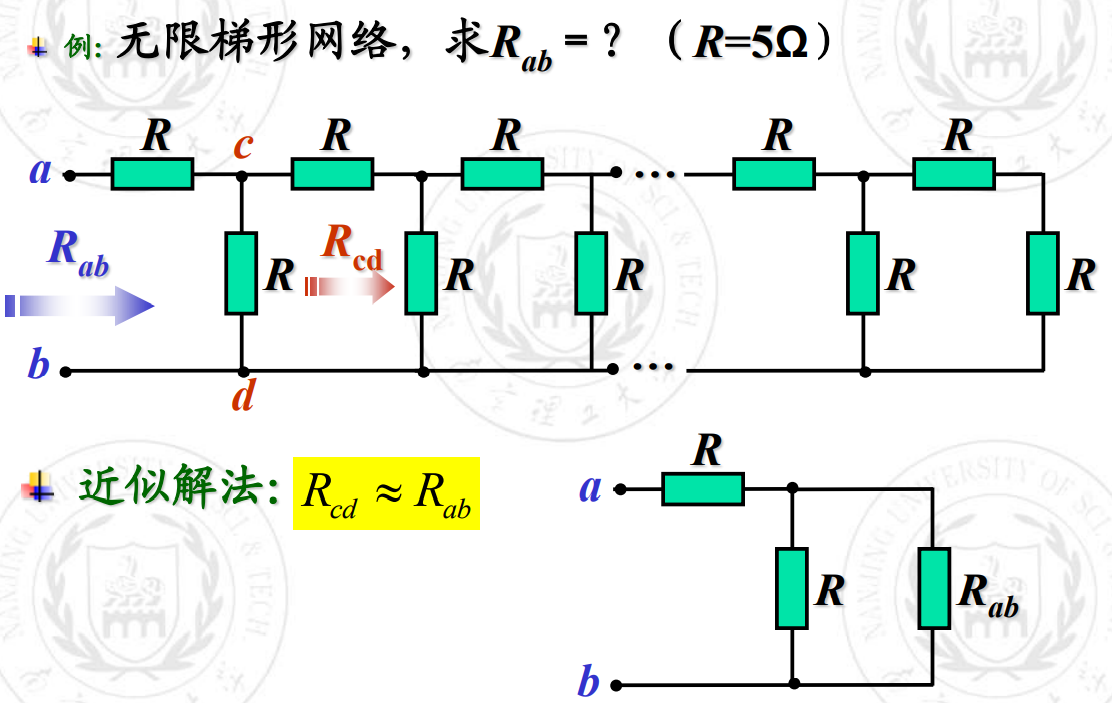
要看比较清晰的解法请戳：https://jingyan.baidu.com/article/1612d500055731a20e1eeeaa.html

$Y-\Delta$​(星-三角变换)

1. Y形等效△形公式：

$$\begin{array}{l} R_{12}=\frac{R_{1} R_{2}+R_{2} R_{3}+R_{3} R_{1}}{R_{3}} \\ R_{23}=\frac{R_{1} R_{2}+R_{2} R_{3}+R_{3} R_{1}}{R_{1}} \\ R_{31}=\frac{R_{1} R_{2}+R_{2} R_{3}+R_{3} R_{1}}{R_{2}} \end{array}$$

2. △形等效Y形公式：

$$\begin{array}{c} R_{1}=\frac{R_{12} R_{31}}{R_{12}+R_{23}+R_{31}} \\ R_{2}=\frac{R_{12} R_{23}}{R_{12}+R_{23}+R_{31}} \\ R_{3}=\frac{R_{23} R_{31}}{R_{12}+R_{23}+R_{31}} \end{array}$$

3. 文字描述就是

$$三角形联结电阻= \frac {星形联结的不相邻电阻} {星形联结电阻两两乘积之和}$$

$$星形联结的电阻= \frac {三角形联结的电阻之和} {三角形联结的相邻电阻的乘积}$$

4. 假若联结中三个电阻相等，则有以下的特殊关系：

$$R_{Y}=\frac{1}{3} R_{△}$$

电源等效

等效是一种丢失信息的过程。

首先要说明一点，就是独立源具有和我们的理想电路模型有等效对应。
独立电流源相当于无限大电阻，或断路;
独立电压源相当于导线，或短路。
它们二者所提供的电压、电流可以认为是这两种理想模型的附加属性。也就是说，独立电流源是一个“电流确定的断路支路”，独立电压源是一个“电压确定的导线”
在分析外电路时，并在电压源两端网络无效，串在电流源支路的网络无效。

电压源

n个独立电压源串联，仍然相当于一条导线，其上短通性质并不改变，仍然为独立源。这时的等效电压源的电压相当于所有电压源电压的代数和。

多个电压源可以并联，但是只有当电压相等时才允许同极性并联。

电压源跟啥并联，啥就可以拍屁股走人，因为最后都会被等效成一个电压没变的等效电压源。但是当算输出电流的时候还得回来，帮这个破电压源算一下并联之后的电流跟之前的大不同。

电流源

独立电流源并联，多个断路并在一起仍然不能导通，所以仍然是独立电流源。这时输出的总电流是所有电流源输出电流之和。

n个电流相等、极性相同的独立电压源串联时，在串联支路中，一断则断。因而性质等同于断路，为一个没变化的独立电流源。

电流源跟啥并联，啥就可以拍屁股走人，因为最后都会被等效成一个电流没变的等效电流源。但是当算输出电压的时候还得回来，帮这个破电流源算一下串联之后的电压跟之前的大不同。

电压源和电流源组合一下呢？

先试试电压源和电流源串联。
因为电压源的外电流已经因为电流源而确定，所以相当于对外性质没有变化的独立电流源。
另外，独立电压源在这里就相当于一个虚拟电阻，可以分担提供一部分电压，所以原来的独立电流源上电压会减小。
这个电压也是独立电压源唯一的作用。

然后是电压源和电流源的并联。
并联中只要一个支路为短路，一短则短。故为电压源，并入一个电流源后端口性质不变。同样地，电流源的目的是提供一部分电流，电压源的电流减小。

总结

元件（或电路）与理想电压源并联，元件（或电路）对外界不起作用，可以断开，只保留电源。
元件（或电路）与理想电流源串联，元件（或电路）对外界不起作用，可以断开，只保留电源。
电压源和电流源串联等效为电流源，电压源和电流源并联等效为电压源。

实际源的等效变换

两类实际电源等效转换的条件是

$$R_s=\frac{1}{G_s}或u_s=R_si_s$$

变换时要注意极性相同。

含受控源的电路

实际电源的等效方法依然对受控源有效，但是要保护控制量完整不被破坏。所以就算要让受控源支路参与等效变换，也别让控制支路搅这趟浑水。

输入电阻：输入电阻$R_i$等于无独立源的一端口网络在端口处外加电压$u$和端口处外标有电压$u$的 “+” 号端钮输入的电流$i$之比。
一个只含电阻的一端口网络的输入电阻永远不会是负值。但当含有受控源时，就有可能是负数了。

那输出电阻是啥？
从网上找了点资料来看看。

输入电阻：

从放大电路的输入端看进去的等效电阻称为放大电路的输入电阻。从放大电路输入端看，等效为一个纯电阻$R_i$。输入电阻$R_i$的大小等于外加输入电压与相应的输入电流之比。

输入电阻这项技术指标描述放大电路对信号源索取电流的大小。
通常希望放大电路的输入电阻越大越好，$R_i$越大，说明放大电路对信号源的索取的电流越小。放大器输入端得到的信号电压也越大，即信号源电压衰减的少。

理论基础：$U_s=（R_s+R_i）×I_i$。Rs为信号源内阻，Ri为放大器输入电阻。

因此作为测量信号电压的示波器、电压表等仪器的放大电路应当具有较大的输入电阻。对于一般的放大电路来说，输入电阻当然是越大越好。

如果想从信号源取得较大的电流，则应该使放大器具有较小的输入电阻。
输出电阻用来衡量放大器在不同负载条件下维持输出信号电压（或电流）恒定能力的强弱，称为其带负载能力。

输出电阻：

当放大器将放大了的信号输出给负载电阻$R_L$时，对负载$R_L$来说，放大器可以等效为具有内阻$R_o$的信号源，由这个信号源向$R_L$提供输出信号电压和输出信号电流。$R_o$称为放大器的输出电阻，它是从放大器输出端向放大器本身看入的交流等效电阻。

如果输出电阻$R_o$很小，满足$R_o<<R_L$条件，则当$R_L$在较大范围内变化时，就可基本维持输出信号电压的恒定。反之，如果输出电阻$R_o$很大，满足$R_o>>R_L$条件，则当$R_L$在较大范围内变化时，就可维持输出信号电流的恒定。
如手机电池，它的内阻可以等效看作输出电阻，用了几年后，内阻高了，也就要报废了，因为带不动外面的东西了。
电压放大和互阻放大电路，即输出为电压信号的放大电路，$R_o$越小，负载$R_L$对的变化对输出信号$V_o$的影响越小。而且只要负载$R_L$足够大，信号输出功率一般较低，能耗也较低。多用于信号的前置放大和中间级放大。对于一般的放大电路来说，输出电阻当然越小越好。
电流放大和互导放大电路，即输出为电流信号的放大电路，与受控电流源并联的$R_o$越大，负载$R_L$的变化对输出电流$I_o$的影响越小。则与前两种相比当供电电源相同时，可得到较大输出电流信号，所以功率可能到达较大的值，对供电电源的能耗较大。通常用于电子系统的输出级，可作为各种输出物理变量变换器（如音响系统的扬声器，动力系统的电动机等）的驱动电路。

做题技巧

1. 求等效电阻
   找串并联关系，捋清楚电路图。捋不清楚可以借助于字母标注法和元件的拉伸，实在不行就去找Y和三角型电阻结构，尽量紧着仨电阻阻值相等的情况来。

2. 求最简电路

   删掉无效元件：串入电阻(电压源)对电流源没有影响，并入电阻(电流源)对电压源没有影响。
   电源转换：实际电压源和实际电流源互化。受控源也可以进行类似独立源的操作。
   电表分裂法：
   
   退字诀：复杂的情况还是要回到最初的伏安特性上去。