CC Computer Science:发展史、二进制和逻辑门
Crash Course Computer Science笔记(一)
课程链接:https://www.bilibili.com/video/av21376839?p=3
字幕仓库:https://github.com/1c7/crash-course-computer-science-chinese
电子计算机的发展史
-
电子计算机元器件变化:继电器→真空管→晶体管
-
计算机的出现背景:
20 世纪人口暴增,科学与工程进步迅速,航天计划成形。以上导致数据的复杂度急剧上升、计算量暴增,对于计算的自动化、高速有迫切的需求。
-
电子计算机的发展:
- 1945 年 哈佛马克 1:使用继电器,用电磁效应,控制机械开关,缺点为有磨损和延迟。
继电器是用电控制的机械开关。继电器里,有根"控制线路",控制电路是开还是关,“控制线路” 连着一个线圈,当电流流过线圈,线圈产生电磁场,吸引金属臂,从而闭合电路。
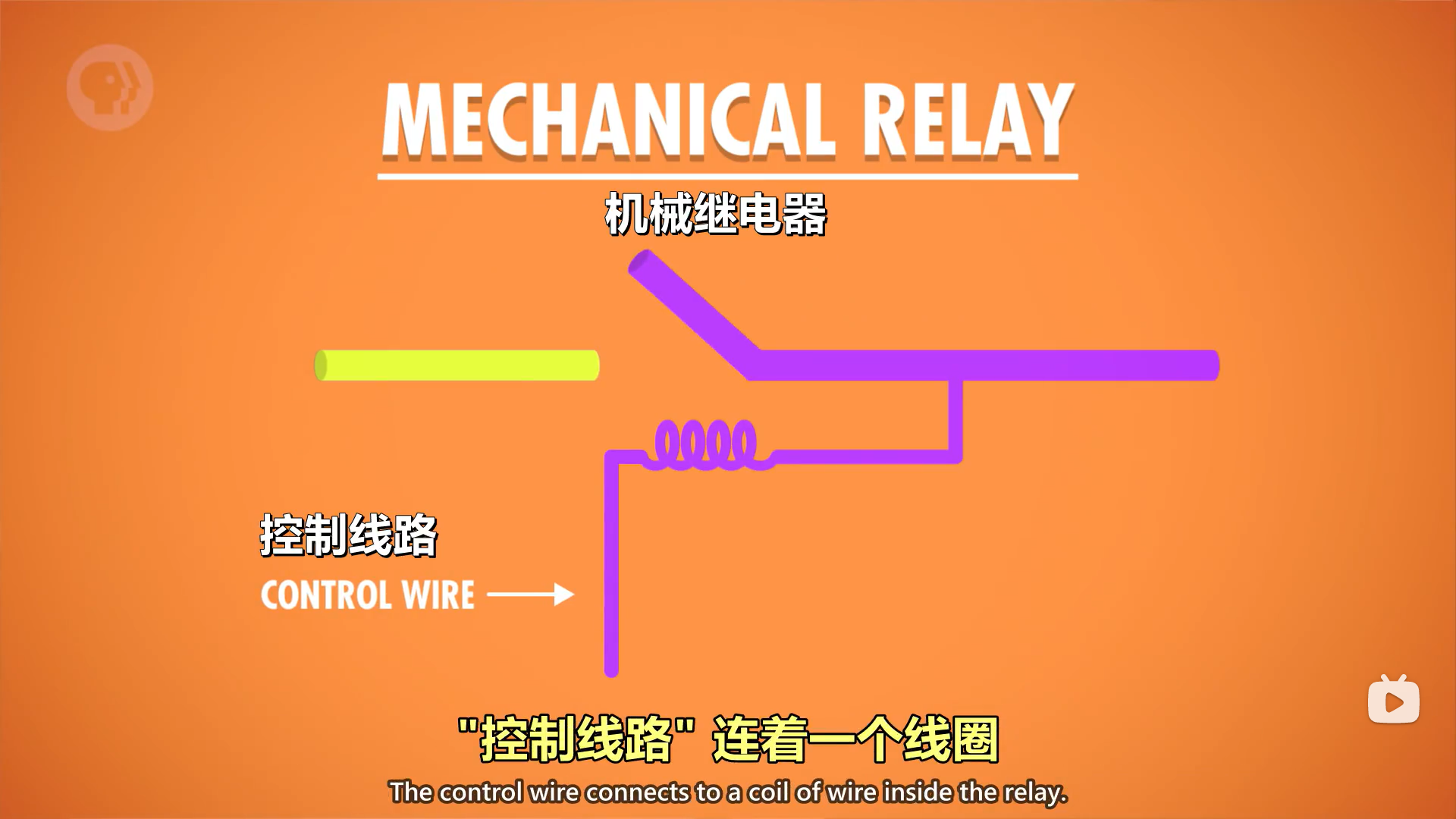
你可以把继电器想成水龙头,把控制线路想成水龙头把。打开水龙头,水会流出来,关闭水龙头,水就没有了。继电器是一样的,只不过控制的是电子,而不是水。
不幸的是,继电器内的机械臂有质量,因此无法快速开关,不足以解决复杂的大问题。
*最早还因为有虫子飞进去导致故障,引申出 bug=故障的意思。
-
1943 年 巨人 1 号:使用真空管(三极管),制造出世界上第一个可编程的计算机。
真空管的起源:在 1904 年,英国物理学家John Ambrose Fleming开发了一种新的电子组件,叫"
热电子管",这是世上第一个真空管。其中一个电极可以加热,从而发射电子,另一个电极会吸引电子,但只有带正电才行。如果带负电荷或中性电荷,电子就没办法被吸引,越过真空区域,因此没有电流。这是一种二极管。为了代替继电器,我们需要的是一个能开关电流的东西。幸运的是,不久之后在 1906 年,美国发明家Lee de Forest在Fleming设计的两个电极之间,加入了第三个 “控制” 电极。

向"控制"电极施加正电荷,它会允许电子流动;但如果施加负电荷,它会阻止电子流动。因此通过控制线路,可以断开或闭合电路。
真空管的使用,意味着更快的开关速度和更少的磨损,但容易烧坏。
-
1946 年 ENIAC:第一个电子通用数值积分计算机。
-
1947 年 晶体管出现,使用的是固态的半导体材料,相对真空管更可靠。
-
1950s 空军 ANFSQ-7: 真空管到达计算极限。
-
1957 年 IBM 608: 第一个消费者可购买的晶体管计算机出现。
晶体管的诞生:1947 年,贝尔实验室科学家发明了晶体管。一个全新的计算机时代诞生了!
晶体管,就像之前提过的"继电器"或"真空管",它是一个开关,可以用控制线路来控制开或关。晶体管有两个电极,电极之间有
一种材料隔开它们,这种材料有时候导电,有时候不导电,这就是半导体。控制线连到一个 “门” 电极,通过改变 “门” 的电荷,我们可以控制半导体材料的
导电性,来允许或不允许电流流动。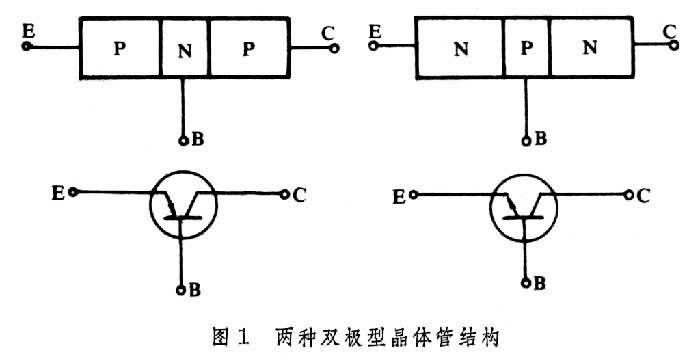
比起玻璃制成的真空管,晶体管是固态的(就是电路元件里三根脚,上边是半圆柱的小黑块),所以更小、更便宜。到了这个计算机时代,我们可以让电路开闭得非常快。
如今,计算机里的晶体管小于 50 纳米,而一张纸的厚度大概是 10 万纳米。
布尔逻辑与逻辑门
计算机为什么使用二进制:
- 计算机的元器件晶体管只有 2 种状态,通电(1)&断电(0),用二进制可直接根据元器件的状态来设计计算机。
- 而且,数学中的“布尔代数”分支已经成熟,可以用 True 和 False(可用 1 代表 True,0 代表 False)进行逻辑运算,代替实数进行计算。
- 计算的状态越多,信号越容易混淆,影响计算。对于当时每秒运算百万次以上的晶体管,信号混淆是特别让人头疼的。
布尔代数&布尔代数在计算机中的实现
-
变量:没有常数,仅 True 和 False 这两个变量。
-
三个
基本操作:NOT/AND/OR。 -
为什么称之为“门”:控制电流流过的路径
1)NOT 操作:
-
命名:称为
NOT 门/非门。 -
作用:将输入布尔值反转。输入的 True 或 False,输出为 False 或 True。
-
晶体管的实现方式:
上面的线当作输出,控制极的线当作输入,如果打开 输入,电流可以流过然后 “接地”,输出就没有电流,所以输出是 off。当输入是 off,电流没法接地,就流过了输出,所以输出是 on。
如果用水来举例,就像家里的水都从一个大管子流走了,打开淋浴头一点水也没有。(请看我的魔幻画)
1
2
3
4
5| |
| |______________output
| ___________________
input|--|——————————|--
| |
-
半导体通电 True,则线路接地,无输出电流,为 False。
-
半导体不通电 False,则输出电流从右边输出,为 True。
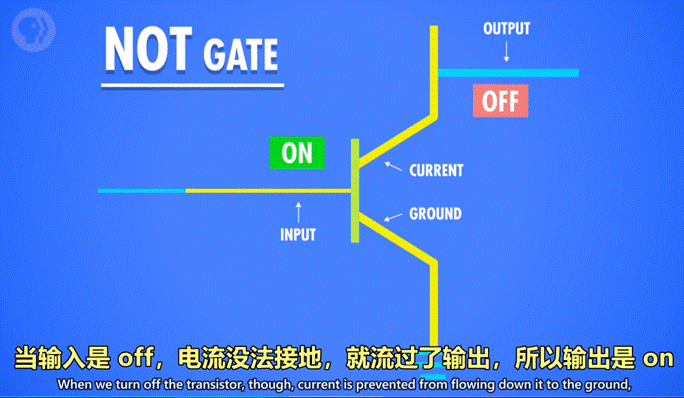
2)AND 操作
-
命名:
AND 门/与门 -
作用:由 2 个输入控制输出,仅当 2 个输入 input1 和 input2 都为 True 时,输出才为 True,2 个输入的其余情况,输出均为 False。
*可以理解为,2 句话(输入)完全没有假的,整件事(输出)才是真的。
真值表:
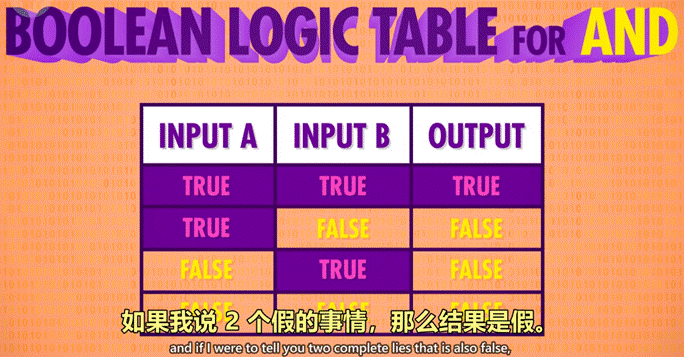
-
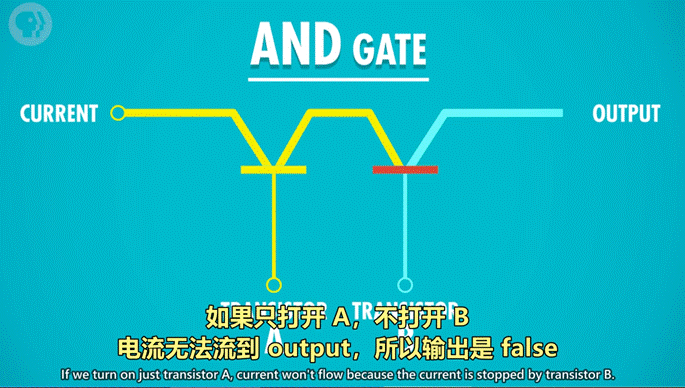
用晶体管实现的方式:
串联两个晶体管,仅当 2 个晶体管都通电,输出才有电流(True)
3)OR 操作
-
命名:OR 门/或门
-
作用:由 2 个输入控制输出,只要其中一个输入为 True,则输出 True。
*有真则真。

-
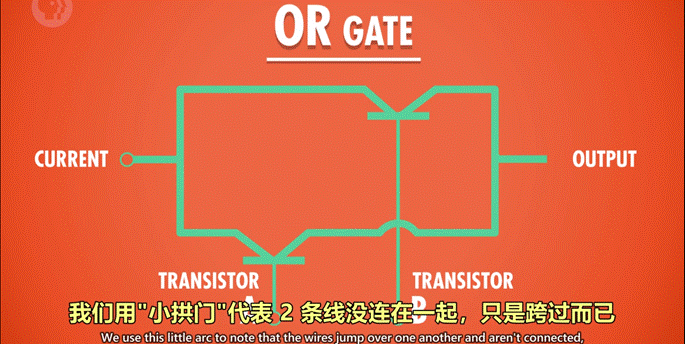
用晶体管实现的方式:
使用 2 个晶体管,将它们并联到电路中,只要有一个晶体管通电,则输出有电流(True)。
特殊的逻辑运算——异或
-
命名:XOR 门/异或门
-
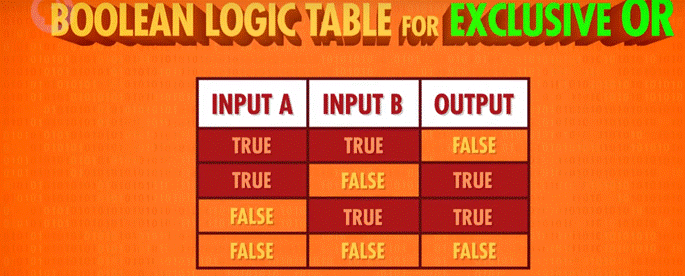
作用:2 个输入控制一个输出。当 2 个输入均为 True 时,输出 False,其余情况与 OR 门相同。
*不同则真。
*打个不恰当的比喻,就像直人们认为1和1,0和0,TTL和PPL们是无法拥有幸福的,至少在他们的yy里。
-
图示:
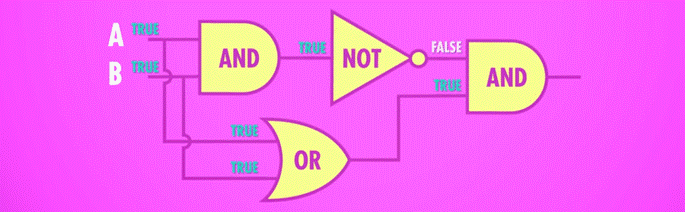
因为XOR的真值表除了第一行都和OR差不多,所以我们只需要把全是1的情况从满足OR门的情况里踢出去。
先用一个 OR 门,将其与 AND 门并联,AND 门与 NOT 门串联,最后让 NOT 与 AND 门并联,获得输出。
下图是两个1的情况:
逻辑门的符号表示
- 作用:将逻辑门简化,将逻辑门用于构建更大的组件,而不至于太复杂。
- 图示:
-
非门:用三角形+圆圈表示(头顶有球球的松树)
-
与门:用 D 型图案表示(半个胶囊)
-
或门:用类似 D 向右弯曲的图案表示(一个笑脸:)
-
异或门:用或门+一个圆弧表示(是一个带双下巴的笑脸 :))




二进制
二进制的原理,存储单元 MB/GB/TB 解释
计算机中的二进制表示:
单个数字 1 或 0,1 位二进制数字命名为位(bit),也称 1 比特。
字节(byte)的概念:
1 byte=8 bit,即 1 byte 代表 8 位数字。最早期的电脑为八位的,即以八位为单位处理数据。为了方便,将八位数字命名为 1 字节(1 byte).
十进制与二进制的区别:
- 十进制有 10 个数字,0-9,逢 10 进 1(不存在 10 这个数字),则每向左进一位,数字大 10 倍。
- 二进制有 2 个数字,0-1,逢 2 进 1,(不存在 2 这个数字),则每向左进一位,数字大 2 倍。
如何进行二进制与十进制联系起来:
将十进制与二进制的位数提取出来,编上单位:
eg.二进制的 (从右往左数)
eg.十进制的
二进制的运算:
相同的位数相加,逢 2 进 1

byte 在电脑中的单位换算:
1 KB=2^10 byte = 1024 byte(用于数据流时) =1000 byte(用于存储时)
1 TB=1000 GB
1 GB=十亿字节=1000 MB=10^6 KB
32 位与 64 位电脑的区别
32 位的最大数为 43 亿左右。
32 位能表示的数字: 到 ,一共个数。
64 位的最大数为
正数、负数、正数、浮点数的表示
1)计算机中表示数字的方法
-
整数:
表示方法:
-
第 1 位:表示正负 1 是负,0 是正(补码)
-
其余 31 位/63 位: 表示实数
-
浮点数(Floating Point Numbers):
定义:小数点可在数字间浮动的数(非整数)
表示方法:IEEE 754 标准下
用类似科学计数法的方式,存储十进制数值
- 浮点数=有效位数*指数
- 32 位数字中:第 1 位表示正负,第 2-9 位存指数。剩下 23 位存有效位数
eg. 625.9=0.6259(有效位数)(指数)

用来表示字符的ASCⅡ码(重要)
-
全称:美国信息交换标准代码
-
作用:用数字给英文字母及符号编号
-
内容:7 位代码,可存放 128 个不同的值。
-
图示:
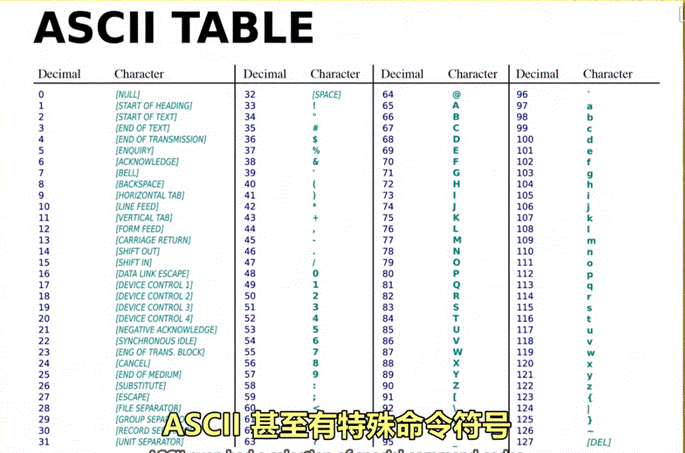
UNICODE,统一所有字符编码的标准
-
诞生背景:1992 诞生,随着计算机在亚洲兴起,需要解决 ASCⅡ不够表达所有语言的问题。
为提高代码的互用性,而诞生的编码标准。
-
内容:UNICODE 为 17 组的 16 位数字,有超过 100 万个位置,可满足所有语言的字符需求。
算术逻辑单元
什么是算术逻辑单元
1 命名:简称 ALU,Arithmetic&Logic Unit
2 组成:ALU 有 2 个单元,1 个算术单元和 1 个逻辑单元(Arithmetic Unit 和 Logic Unit)
3 作用:计算机中负责运算的组件,处理数字/逻辑运算的最基本单元。
算术单元
它负责计算机里的所有数字操作,比如加减法,它还做很多其他事情,比如给某个数字+1,这叫增量运算,我们之后会说。
现在要理解它是如何进行计算的,换句话说——如何把两个数字相加?
我们可以用单个晶体管一个个拼,把这个电路做出来,但很快就会复杂得难以理解。所以与其用晶体管,我们不如用更高层的抽象——逻辑门来做。
最简单的加法电路,是拿 2 个 bit 加在一起(bit 是 0 或 1),这就是半加器。要想加更多位,我们就要组装全加器。
所以算术单元的雏形在我们脑海里出现了:
1)基本组件:
-
由半加器、全加器组成
-
半加器、全加器由 AND、OR、NOT、XOR 门组成
2)加法运算
-
组件:AND、OR、NOT、XOR 门
-
元素:输入 A,输入 B,输出(均为 1 个 bit,即 0 或 1)
-
半加器:
- 作用:用于计算个位的数字加减。
- 输入:A,B
- 输出:总和(SUM),进位(CARRY)
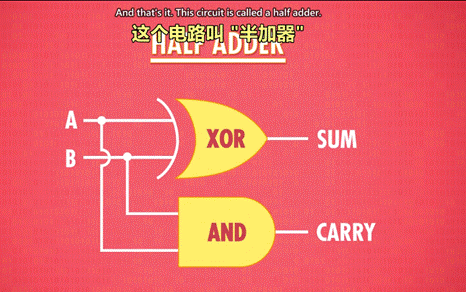
- 抽象(把半加器封装成一个单独组件):
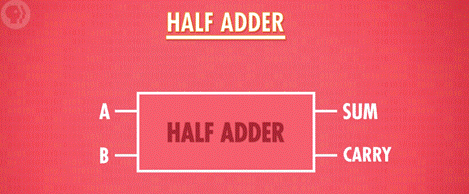
-
三位全加器:
作用:用于计算超过 1 位的加法(ex:1+1+1),由于涉及进位,因此有 3 个输入(C 充当进位)。
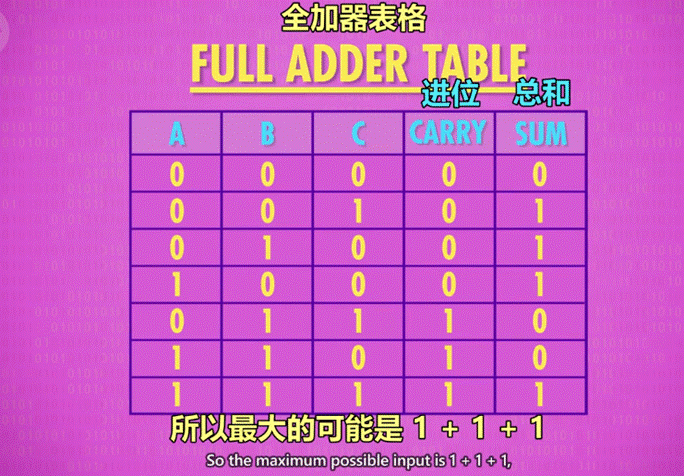
原理图示:
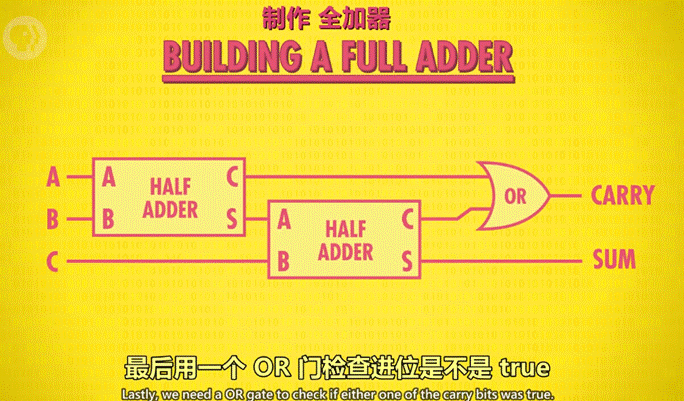
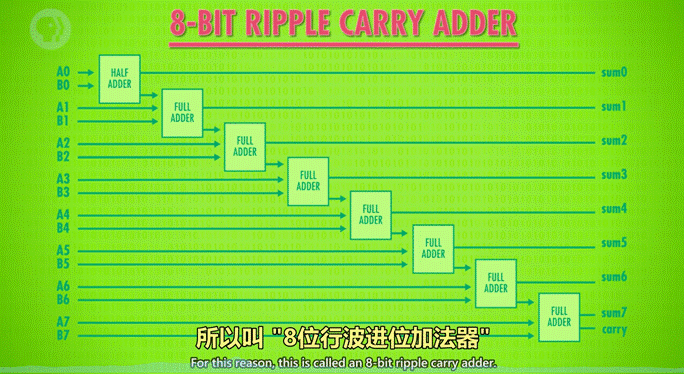
3)如何用半加器与全加器做 8 位数的加法
说明:以 8 位行波加法器为例
-
用半加器处理第 1 位数(个位)的加法,得到的和为结果的第 1 位。
-
将输出的进位,输入到第 2 位用的全加器的输入 C 中。
-
将第 2 位的 2 个数用全加器计算,得到的和为结果的第 2 位(sum)。
-
将第 2 位计算的进位连接到百位的全加器输入 C 中。
-
在第 3-8 位上,循环第 3-4 步的操作。
*现在电脑使用的加法器叫“超前进位加法器”
4)算术单元支持的其他运算
便宜的ALU没有乘除法单元。

溢出的概念
内容:在有限的空间内,无法存储位数过大的数,则称为溢出。
比如吃豆人的第256关会乱码。
说明:第 8 位的进位如果为 1,则无法存储,此时容易引发错误,所以应该尽量避免溢出。
逻辑单元
作用:执行逻辑操作,如 NOT、AND、OR 等操作,以及做简单的数值测试。
ALU 的抽象
1)作用:ALU 的抽象让工程师不再考虑逻辑门层面的组成,简化工作。
2)图示:像一个大“V”。

3)说明:
图示内容包括:
- 输入: A,B(都是8 bits),以及4位的操作代码
- 输出:8位的结果 和 一堆1位的标志(flags)
- 标志:溢出标志、零标志和负数标志等(这三个是都有的)
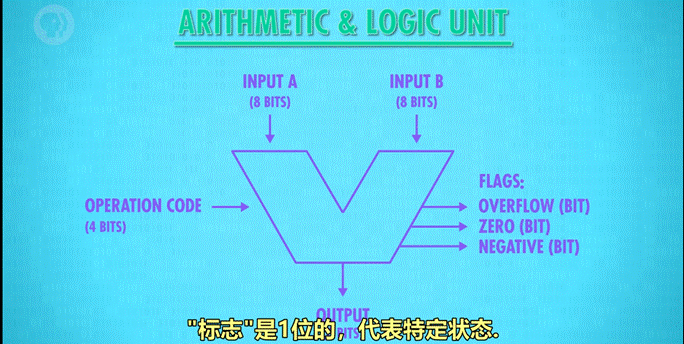
到这里就很突兀地结束了。这篇文章只做了第2-5集的内容,计划做笔记到第11集左右,挑着记。
👋下次见。👋

